参考资料

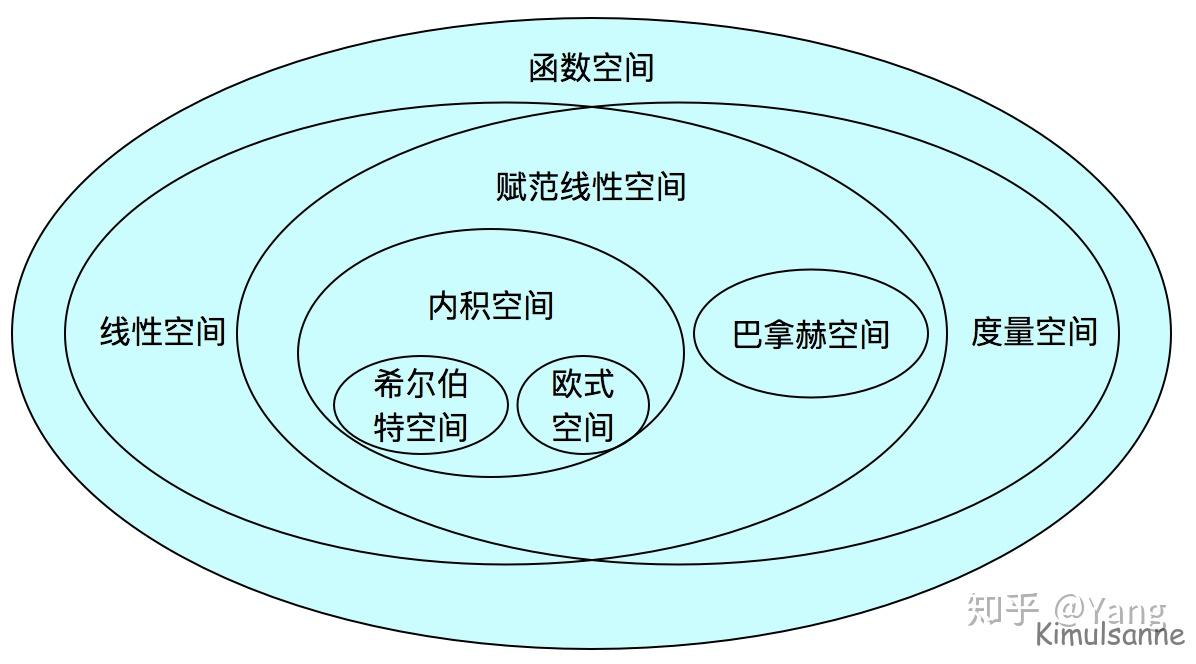
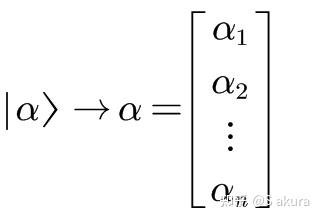
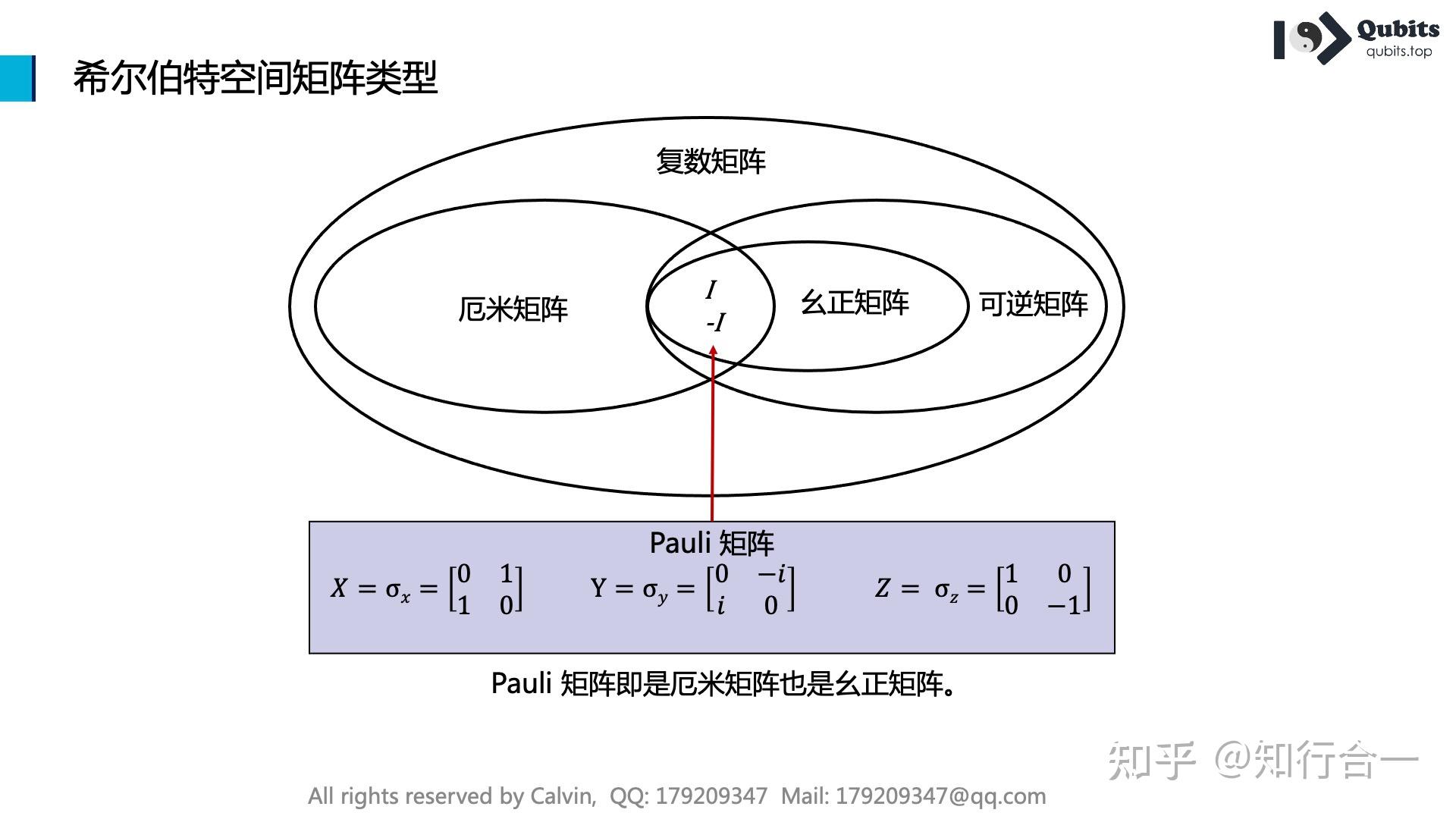
希尔伯特空间是量子力学中一个核心的数学结构，它为量子态的描述和量子系统的演化提供了一个严格的数学框架。在量子力学中，一个量子系统的状态可以用希尔伯特空间中的一个向量来表示，这个向量被称为态矢量或态函数。量子力学的基本原理指出，微观系统的状态由希尔伯特空间的矢量描述，而物理量则由希尔伯特空间的线性厄米算符表示。

希尔伯特空间在量子力学中的应用非常广泛，包括但不限于：

1. 量子态的描述：量子系统的状态可以用希尔伯特空间中的向量来表示，这些向量满足特定的内积关系，允许计算量子态之间的概率幅。

2. 量子演化的表达：量子系统的演化遵循薛定谔方程，这个方程在希尔伯特空间中表述，描述了量子态随时间的变化。

3. 量子测量理论：量子测量过程可以用希尔伯特空间中的投影算子来描述，这些算子将量子系统的状态投影到某个特定的本征态上。

4. 量子纠缠和量子信息：在量子信息科学中，希尔伯特空间的概念被用来描述量子比特的状态和演化，这是量子计算和量子通信的基础。

5. 量子场论：在量子场论中，希尔伯特空间用于描述粒子的产生和湮灭，以及场的量子态。

通过搜索结果，我们可以看到希尔伯特空间在量子力学中的应用是多方面的，它不仅是量子力学的数学基础，而且在量子信息科学、量子计算和量子力学的各个分支中都有广泛的应用。例如，量子比特的状态和演化在量子信息科学中就是通过希尔伯特空间来描述的。此外，希尔伯特空间的理论和应用也在不断拓展，随着量子信息与量子计算领域的不断发展，希尔伯特空间在这些领域的应用也日益重要。

图片来源：量子力学的数学基础 - 百家号