衍生品定价模型如何处理和区分自然条件下类别和个体标的的的差异?
参考资料
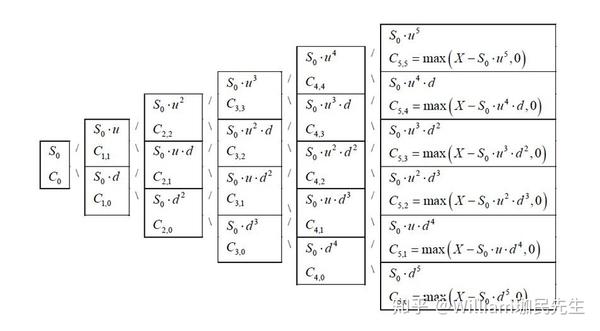
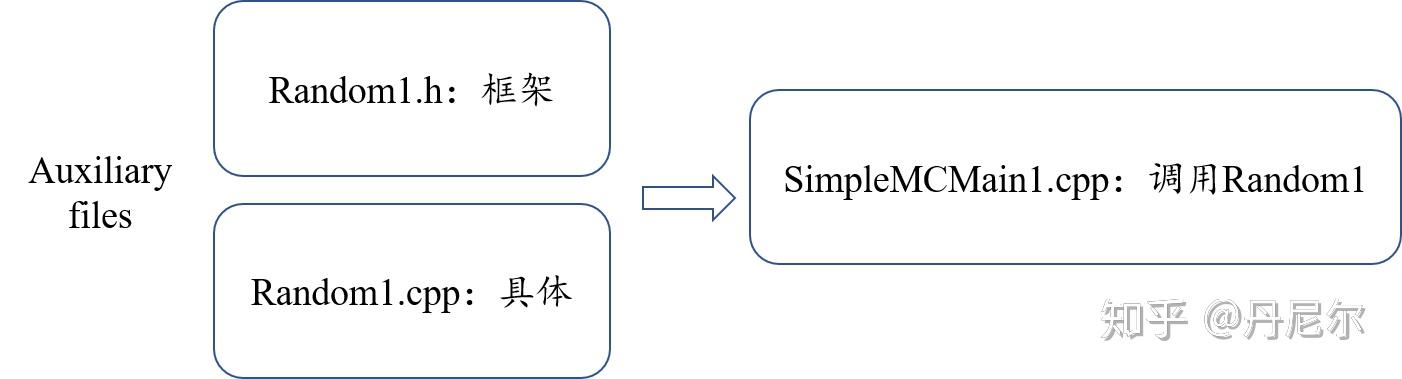


参考资料


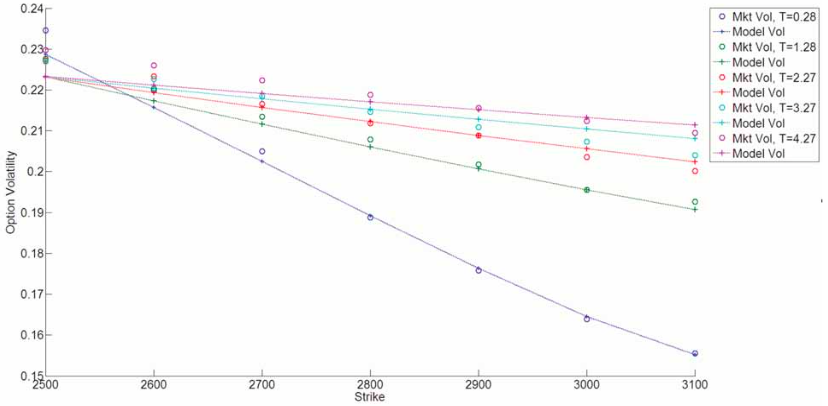
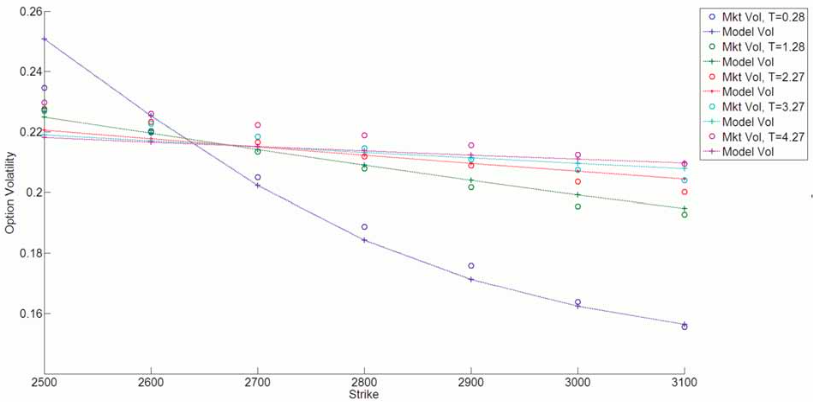
Moonshot回答
在衍生品定价模型中,区分自然条件下的类别和个体标的的差异主要通过以下几个方面来处理:
-
模型选择:不同的衍生品需要使用不同的定价模型。例如,股票期权可能使用Black-Scholes模型,而利率衍生品可能使用Hull-White模型。这些模型根据标的资产的特性和市场条件来设定。
-
参数估计:模型参数需要根据市场数据来估计。例如,波动率是衍生品定价中的关键参数,对于不同类别的标的资产,其波动率的估计方法可能不同。
-
市场数据:定价模型需要依赖市场数据,如股票价格、利率、波动率等。不同类别的标的资产会有不同的市场数据来源和特性。
-
风险中性定价:在定价衍生品时,通常采用风险中性定价方法,这意味着在无套利的假设下,衍生品的价格等于其未来收益的贴现值。
-
数值方法:对于复杂的衍生品,可能需要使用数值方法来求解定价模型,如蒙特卡洛模拟或有限差分法。
-
敏感性分析:对衍生品价格对市场参数变化的敏感性进行分析,以评估不同类别和个体标的资产的风险。
-
监管和市场惯例:在某些情况下,监管要求或市场惯例也会影响衍生品的定价方式。
通过搜索结果,我们可以看到有关衍生品定价模型的讨论,包括Black-Scholes模型、Hull-White模型等,以及如何通过数据驱动的方法来构建更科学的定价模型。这些模型和方法都考虑到了不同类别和个体标的资产之间的差异。例如,李辰旭教授的研究提出了一种数据驱动的金融衍生品定价模型,这种方法可以广泛应用于基于各种类型标的资产的期权。此外,还有讨论关于衍生品定价中模型拟合的重要性,以及如何使用不同的模型来描述客观标的资产。这些信息表明,衍生品定价模型在处理不同类别和个体标的资产时,会采用不同的方法和模型来确保定价的准确性和科学性。