什么是Hessian矩阵，它在多维牛顿法中的作用是什么？
参考资料
Moonshot回答
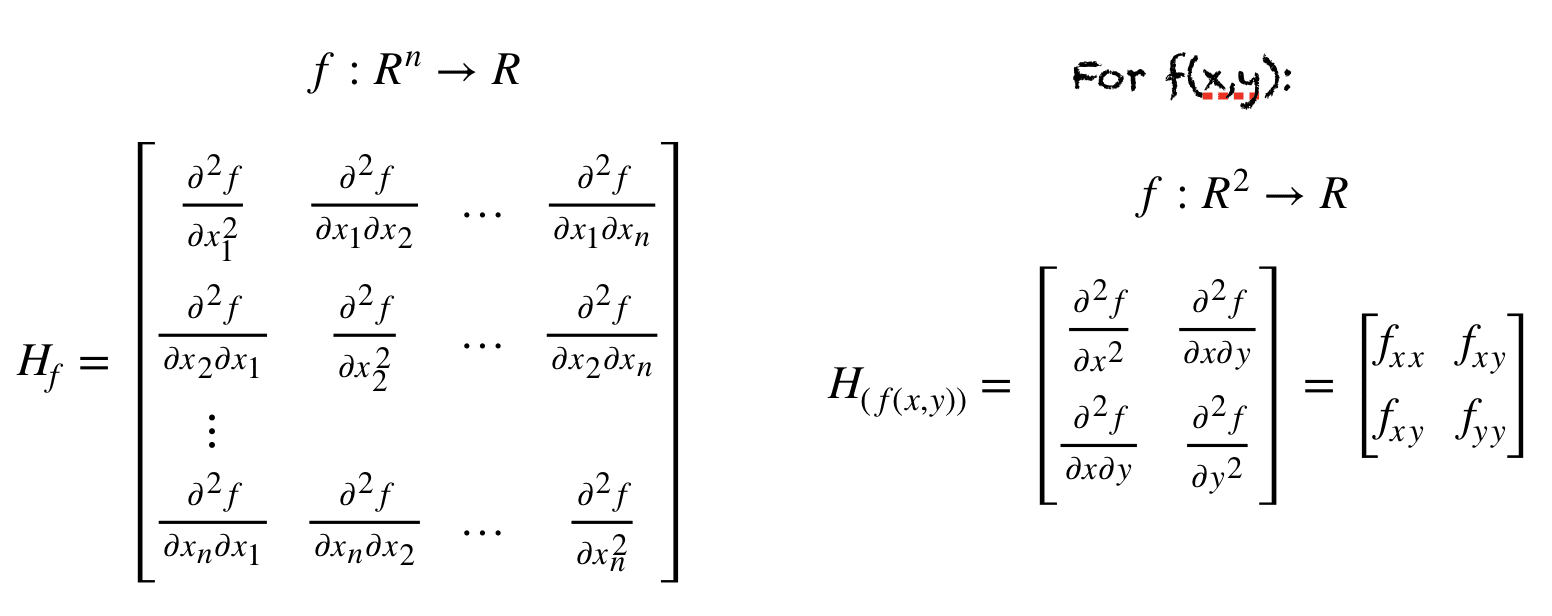
Hessian矩阵是多元函数的二阶偏导数构成的方阵，它在多维牛顿法中扮演着至关重要的角色。多维牛顿法利用Hessian矩阵来确定搜索最优解时的步长和方向，以实现快速收敛。具体来说，Hessian矩阵提供了目标函数曲率的信息，帮助决定在每一步迭代中如何调整参数以更接近最小值。
然而，Hessian矩阵的使用也带来了一些挑战。首先，Hessian矩阵必须正定才能保证算法的收敛，但在非凸问题中，Hessian矩阵可能非正定，导致算法无法收敛。其次，随着问题维度的增加，Hessian矩阵的计算和存储需求急剧增加，这可能导致计算复杂度和资源消耗过大。
为了解决这些问题，研究者们提出了多种改进方法，如拟牛顿法，它通过近似Hessian矩阵来降低计算成本，同时保持较快的收敛速度。此外，还有一些方法专注于保持Hessian矩阵的正定性，以确保算法的稳定性和收敛性。
以下是一些与Hessian矩阵和多维牛顿法相关的图像资源：
这些资源可以帮助更直观地理解Hessian矩阵在多维优化问题中的应用和影响。