希尔伯特空间是什么,为何在数学和物理学中如此重要?
参考资料

参考资料



Moonshot回答
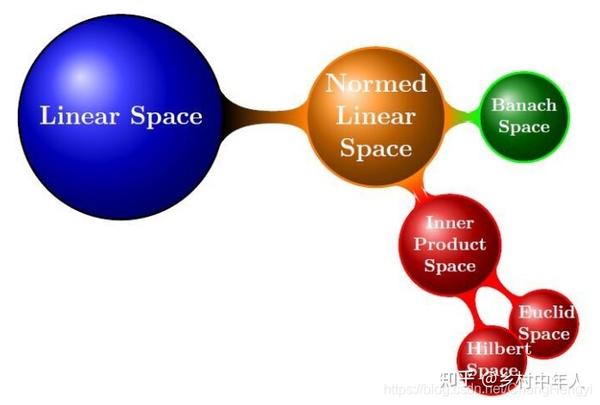
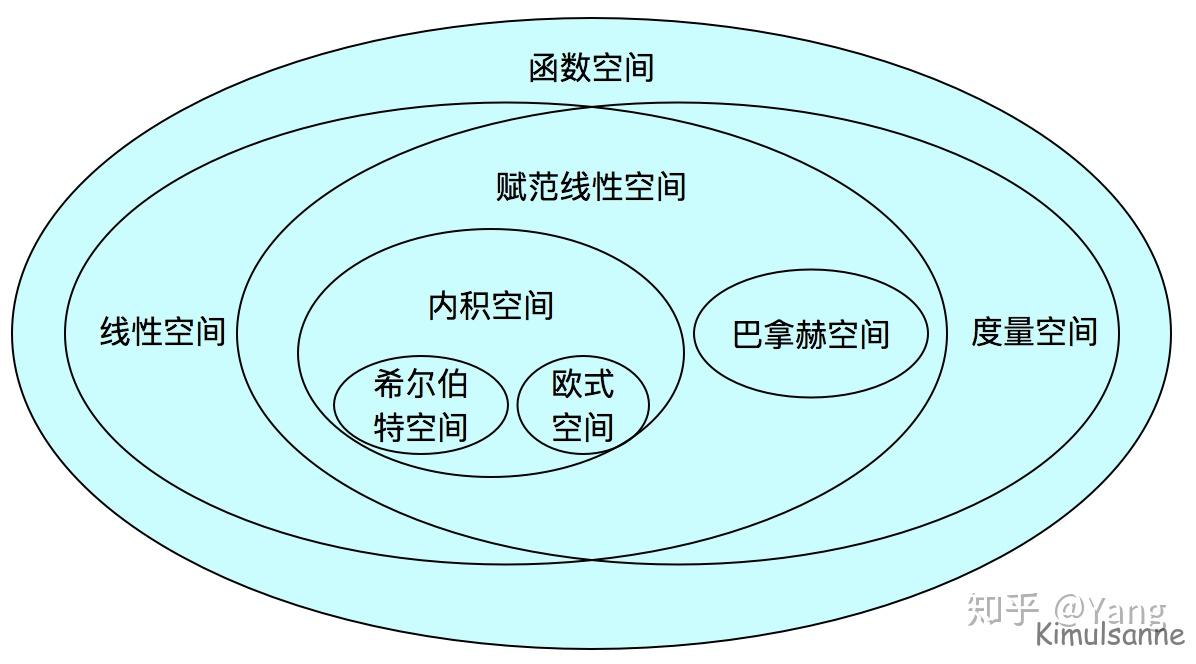
希尔伯特空间是数学中的一个关键性概念,它是一个完备的内积空间。这意味着它是一个配备了内积的向量空间,其中的内积构造推广了欧几里得空间的距离和角的概念。此外,希尔伯特空间中的任意一个元素都可以用空间中的一组基表示,并且空间中任意一个柯西序列的极限也属于这个空间,这称为空间的完备性。
在数学和物理学中,希尔伯特空间之所以重要,原因包括但不限于以下几点:
- 正交性和完备性:希尔伯特空间中的正交性是其重要性质之一,它在许多应用中起到了关键作用。完备性则确保了空间中任意一个柯西序列的极限也属于这个空间,这使得微积分中的许多概念都可以推广到希尔伯特空间中。
- 自反性:希尔伯特空间具有很强的自反性,这意味着空间中的每个元素都可以用空间中的一组基表示。
- 量子力学的基础:冯·诺伊曼可能是最早清楚地认识到希尔伯特空间的重要性的数学家之一,他在进行对量子力学的基础性研究中使用了希尔伯特空间这个概念。量子力学中的态矢量和算符都可以用希尔伯特空间来描述。
- 泛函分析:希尔伯特空间在泛函分析中扮演着核心角色,它为研究无限维空间提供了一个强大的框架。
此外,希尔伯特空间的性质允许定义向量正交、正交和、正交投影的概念,使得柯西-施瓦茨不等式、勾股定理和投影定理在其中成立。这些性质使得希尔伯特空间成为研究物理现象,如波动方程和量子态,的理想工具。因此,希尔伯特空间在数学和物理学的许多领域中都扮演着核心角色。