阿伊姆霍兹方程与波动方程有什么关系,如何将波动方程转化为阿伊姆霍兹方程?
参考资料



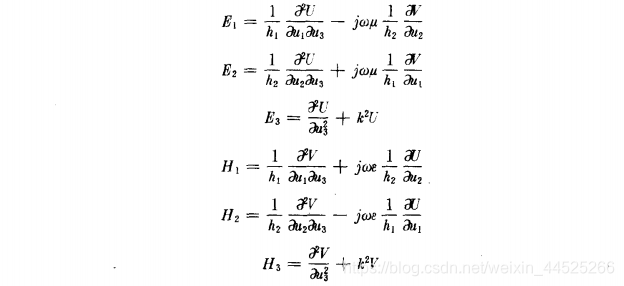
参考资料


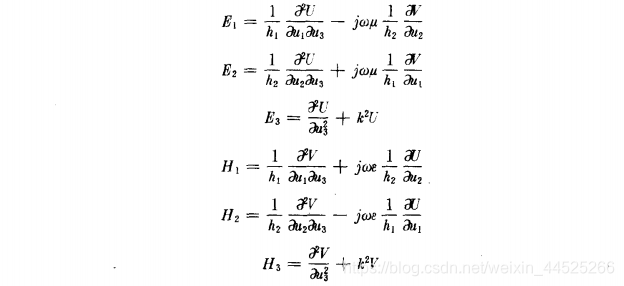

Moonshot回答
阿伊姆霍兹方程(Helmholtz equation)与波动方程(wave equation)之间存在密切的关系。亥姆霍兹方程通常用来描述波在空间中的传播,而波动方程则描述波随时间和空间的变化。具体来说,亥姆霍兹方程可以看作是波动方程在特定条件下的简化形式,当波动方程中的波源或介质特性不随时间变化时,可以将其简化为亥姆霍兹方程。
将波动方程转化为亥姆霍兹方程的过程通常涉及以下步骤:
- 假设波动方程中的波场可以表示为时间和空间部分的乘积,即 $u(\mathbf{r}, t) = U(\mathbf{r})T(t)$。
- 将这个假设代入波动方程,得到两个独立的方程:一个是关于空间变量的亥姆霍兹方程,另一个是关于时间变量的常微分方程。
- 解这两个方程,得到空间和时间的解,然后将它们相乘以得到原始波动方程的解。
例如,对于三维空间中的波动方程 $u_{tt}(\mathbf{r},t) - a^2 \nabla^2 u(\mathbf{r},t) = 0$,通过分离变量法,可以得到空间部分的亥姆霍兹方程 $\nabla^2 U(\mathbf{r}) + k^2 U(\mathbf{r}) = 0$,其中 $k = \frac{a}{2\pi} \omega$ 是波数,$\omega$ 是角频率。
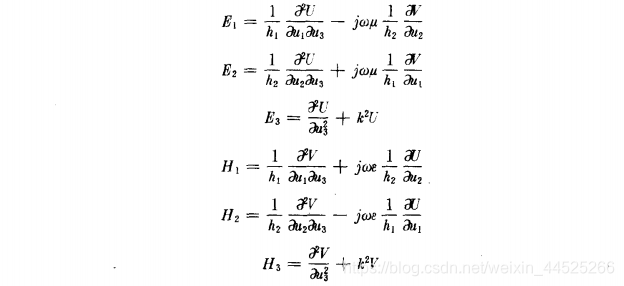
通过这种方式,亥姆霍兹方程在描述波的传播和衍射方面提供了一个非常有用的工具,尤其是在处理静态场或波动在特定条件下的问题时。