拉格朗日恒等式在向量外积（楔积）的计算中扮演着重要角色。它表达了两个向量的点积与外积之间的关系。具体来说，对于任意两个向量 (\mathbf{a}) 和 (\mathbf{b})，拉格朗日恒等式可以表示为：

[ (\mathbf{a} \cdot \mathbf{a}, \mathbf{b} \cdot \mathbf{b}) - (\mathbf{a} \cdot \mathbf{b})^2 = (\mathbf{a} \wedge \mathbf{b}) \cdot (\mathbf{a} \wedge \mathbf{b}) ]

这里，(\mathbf{a} \cdot \mathbf{a}) 和 (\mathbf{b} \cdot \mathbf{b}) 分别是向量 (\mathbf{a}) 和 (\mathbf{b}) 的模长的平方，(\mathbf{a} \cdot \mathbf{b}) 是向量 (\mathbf{a}) 和 (\mathbf{b}) 的点积，而 (\mathbf{a} \wedge \mathbf{b}) 是向量 (\mathbf{a}) 和 (\mathbf{b}) 的外积，其模长等于由这两个向量构成的平行四边形的面积。

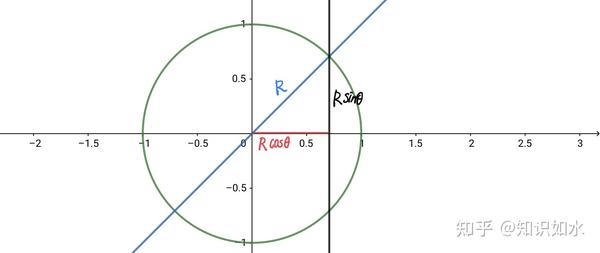
这个恒等式揭示了两个向量的点积的平方与它们构成的平行四边形面积的平方之间的关系。它在计算两个向量的外积的模长时非常有用，因为外积的模长可以通过向量的模长和它们之间夹角的正弦值来计算，即 (|\mathbf{a} \wedge \mathbf{b}| = |\mathbf{a}||\mathbf{b}|\sin\theta)，其中 (\theta) 是向量 (\mathbf{a}) 和 (\mathbf{b}) 之间的夹角。

此外，拉格朗日恒等式也被称为二维勾股定理，因为它类似于勾股定理，即在一个直角三角形中，直角边的平方和等于斜边的平方。在向量的情况下，这个恒等式提供了一种计算两个向量外积模长的方法，这在解决涉及平面、直线和旋转的问题时非常有用。