什么是涵数，如何在量子力学中定义和应用它们？
参考资料
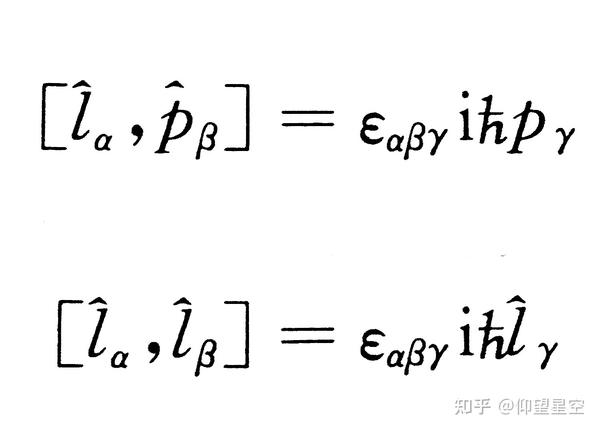
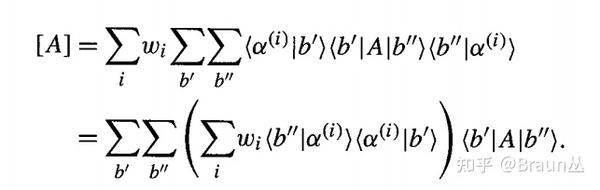
参考资料
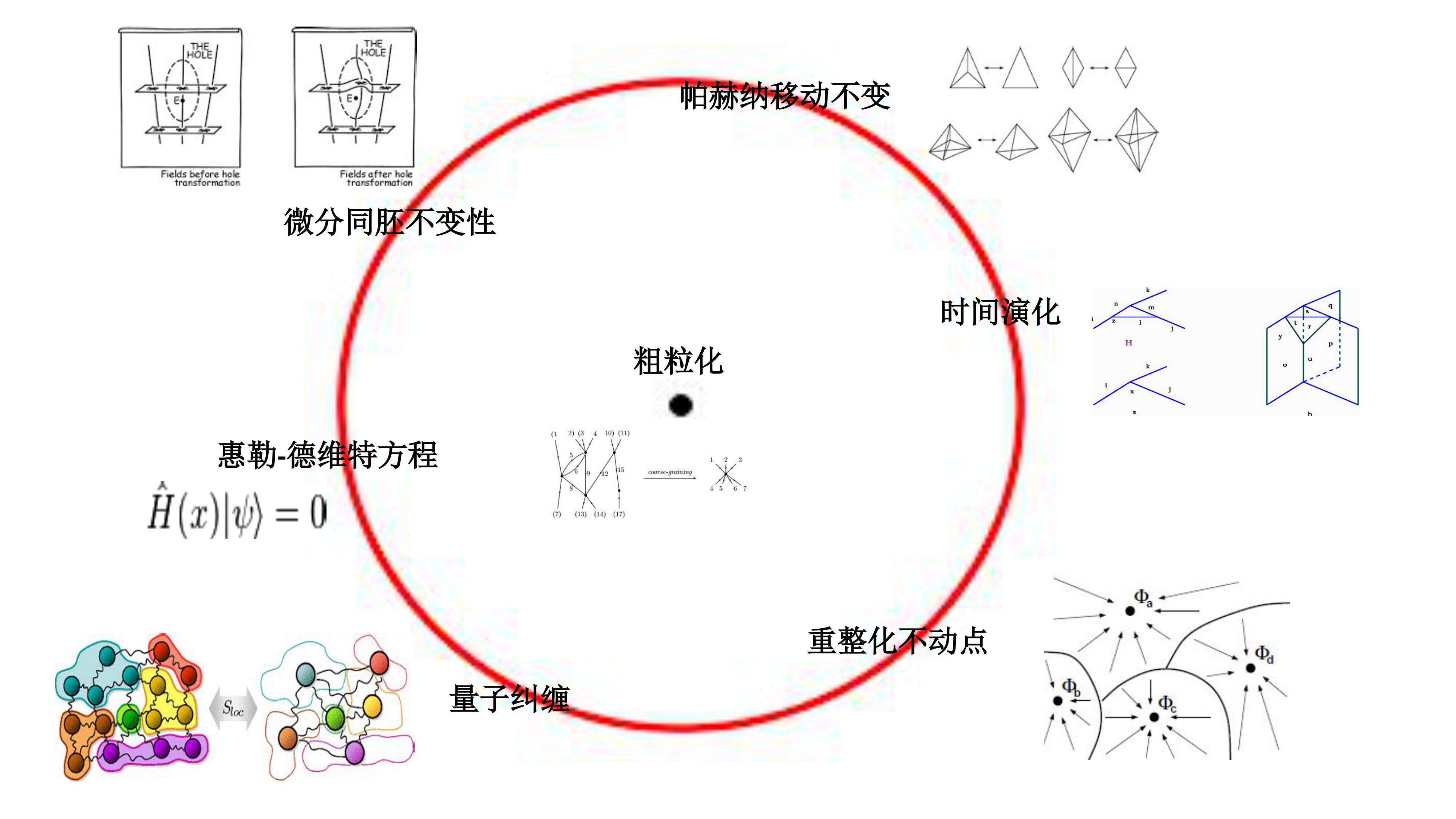
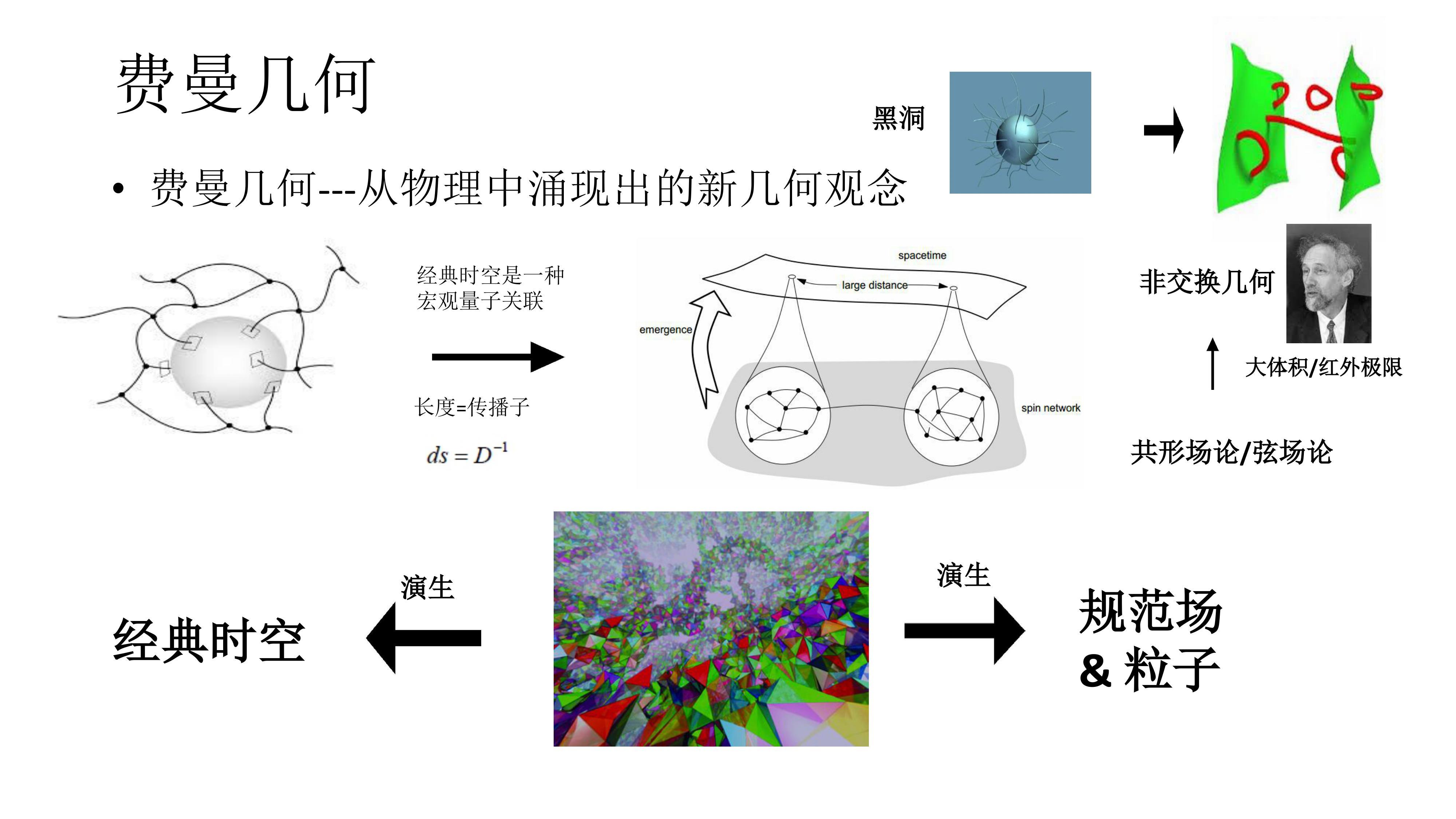
Moonshot回答
涵数在量子力学中通常指的是波函数（Wave function），它是一个复值概率幅，用于描述量子系统的状态。波函数是量子力学的基本概念之一，它包含了我们对量子系统的所有知识。波函数通常表示为Ψ或ψ，是量子系统可能状态的数学描述，其模的平方给出了粒子出现在某个位置或处于某种状态的概率密度。
波函数在量子力学中的应用非常广泛，它可以用来计算粒子的各种物理量，如位置、动量、能量等。通过求解薛定谔方程可以得到系统的波函数，进而预测实验结果。例如，在原子物理学中，波函数可以帮助我们理解电子在原子中的分布情况，解释原子的光谱特性。
量子力学中的波函数定义和应用是该领域的核心内容。波函数的数学表述涉及到复数、线性代数和希尔伯特空间等概念。在不同的表象中，波函数的形式可能不同，但其物理意义是相同的。例如，在位置表象中，波函数描述了粒子在不同位置的概率分布；在动量表象中，波函数描述了粒子具有不同动量的概率分布。
量子力学的波函数在现代科技中有着广泛的应用，包括但不限于半导体器件、激光技术、核磁共振成像（MRI）、量子计算机的开发等。例如，半导体晶体管的工作原理就涉及到量子力学中的波函数概念，而量子计算机则利用量子比特（qubits）的叠加态和纠缠态来进行信息处理，这些都是基于波函数的数学描述和物理解释。
图片展示了量子力学中波函数的概念，其中波函数的模平方表示粒子在不同位置的概率密度。
以上信息综合了来自维基百科、知乎专栏等来源的搜索结果。