参考资料
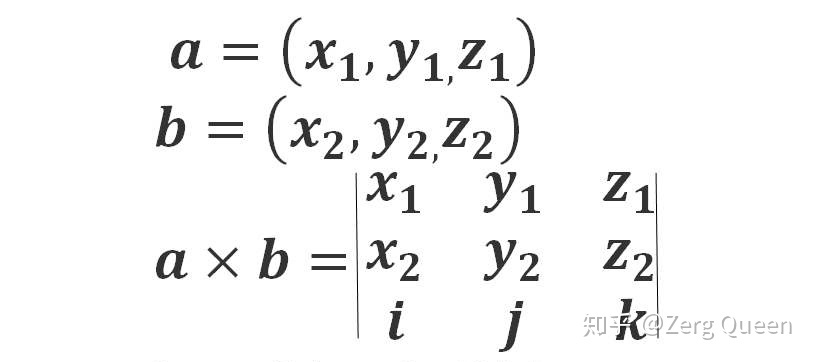


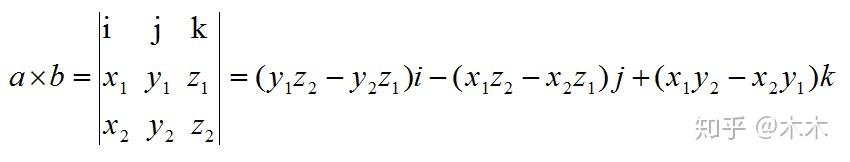
参考资料
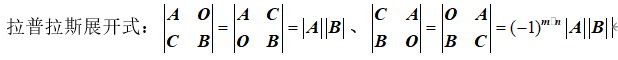


Moonshot回答
行列式在计算两个向量的外积时,特别是在三维空间中,具有重要的几何意义。外积(叉积)的模等于以这两个向量为邻边的平行四边形的面积,这可以通过行列式来表示。例如,在三维空间中,两个向量 (\mathbf{a} = (a_1, a_2, a_3)) 和 (\mathbf{b} = (b_1, b_2, b_3)) 的外积可以通过一个三阶行列式来计算:
[ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 \end{vmatrix} ]
这个行列式的计算结果是一个向量,它垂直于由 (\mathbf{a}) 和 (\mathbf{b}) 张成的平面,并且其模等于由这两个向量形成的平行四边形的面积。
萨赖法则(Sarrus' rule)是用于计算3x3矩阵行列式的一种方法,它通过将矩阵的前两列复制到第三列的右侧,然后计算对角线乘积之差来得到行列式的值。这种方法可以简化为:
[ \text{det}(A) = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{31}a_{22}a_{13} - a_{32}a_{23}a_{11} - a_{33}a_{21}a_{12} ]
拉普拉斯展开法则是一种更通用的方法,用于计算任意阶数矩阵的行列式。它通过选择矩阵的任意一行或一列,然后计算该行或列中每个元素的余子式,并将这些余子式与其对应的元素相乘后求和来得到行列式的值。
在计算两个向量的外积时,行列式提供了一种简洁而强大的工具,允许我们通过代数运算来探索和计算向量之间的几何关系。通过萨赖法则和拉普拉斯展开法,我们可以更深入地理解行列式在向量运算中的应用。