伽玛函数在数学中的主要应用是什么,它是如何定义的?
参考资料

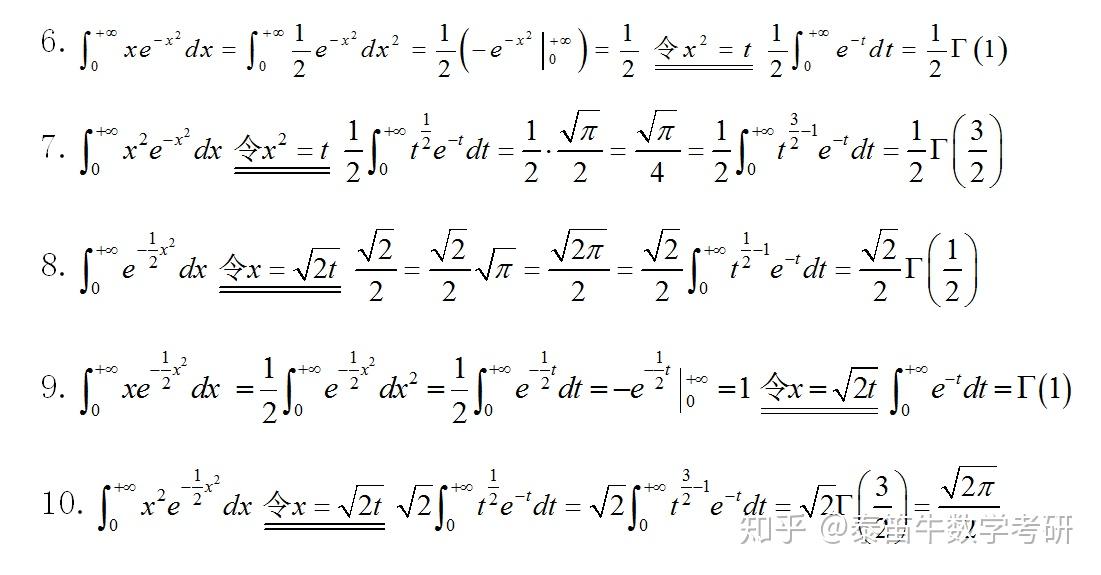
参考资料
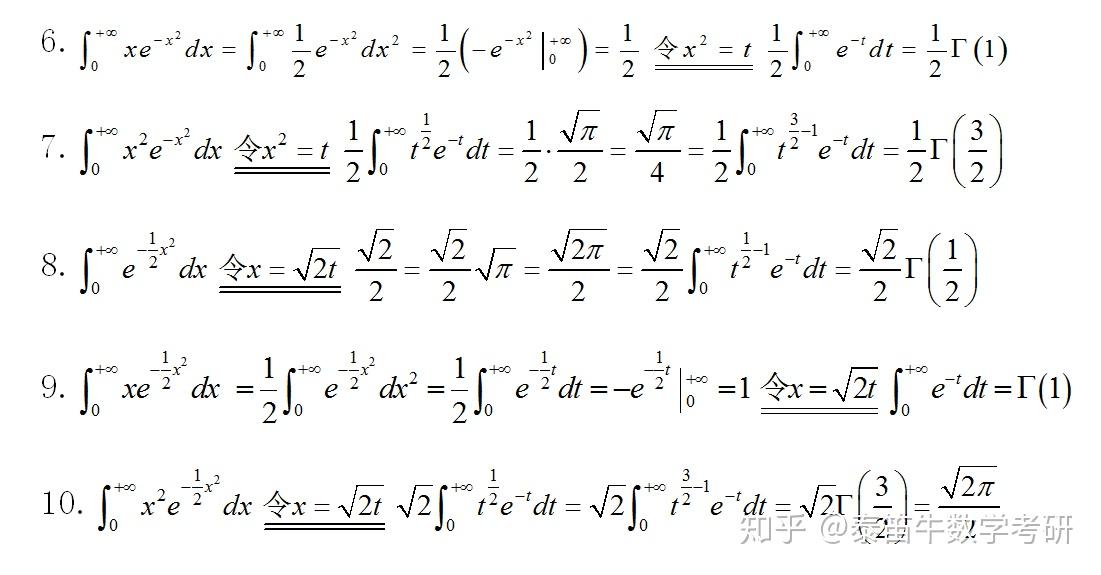

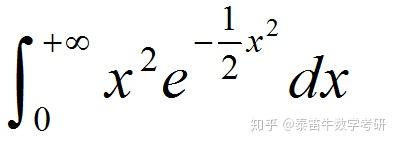
Moonshot回答
伽玛函数(Gamma函数)是阶乘函数在实数和复数域上的扩展。它主要定义为:
[ \Gamma(x) = \int_0^{+\infty} t^{x-1} e^{-t} dt ]
当( x )是非负整数时,伽玛函数的值等于( x-1 )的阶乘。对于复数,伽玛函数通过解析延拓原理定义在除去非正整数的整个复数域上。
伽玛函数在数学中有广泛的应用,包括但不限于:
- 分析学:在研究特殊函数和积分时经常用到。
- 概率论:用于定义伽玛分布和贝塔分布,这些分布在统计学中非常重要。
- 偏微分方程:在解某些类型的偏微分方程时会出现。
- 组合数学:在组合数学中,伽玛函数有助于解决涉及计数和排列的问题。
此外,伽玛函数还出现在n维球体的体积公式中,并且与贝塔函数(Beta函数)有密切联系,后者也用于计算积分。
以下是一些与伽玛函数相关的图像:

继续提问
相关问题
延展性在材料科学中是指什么性质,它是如何定义的?
达朗贝尔算符在Proca方程中有什么作用,它是如何定义的?
解释普朗克常数在量子力学中的重要性,它是如何定义的?
可以列出2004年和2018年张艺谋执导的两部电影及其在日本的票房表现吗?
胡安·庞塞·德莱昂是如何与青春之泉的传说联系在一起的?
如何在write_to_db.sh脚本中确保CSV文件中包含的学生姓名中的特殊字符不会导致SQL查询语句出错?
谁是电影《限时翻供》的导演,除了导演还有哪些人在幕后团队中发挥了重要作用?
为何南方种植园主在1816年关税通过后改变了对关税的态度,并在之后的关税立法中较少支持?
穆罕默德·本·沙特与穆罕默德·阿卜杜勒-瓦哈卜的合作如何奠定了沙特阿拉伯的基础?
湖北国土资源职业学院的师资力量如何,学校采取了哪些措施来提升教师的教学水平?