龙格-库塔法的应用领域包括哪些,它为什么重要?
参考资料

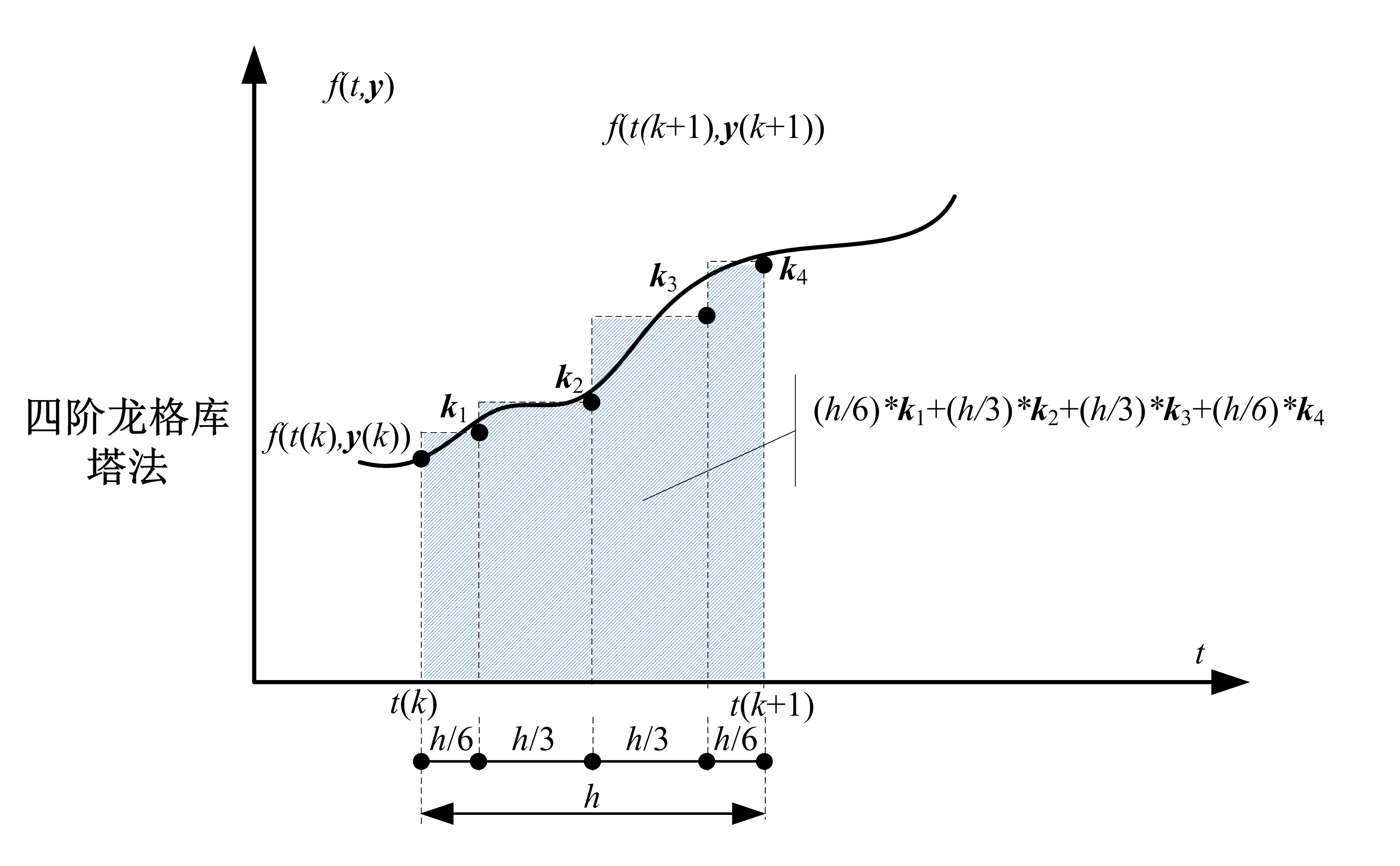
参考资料

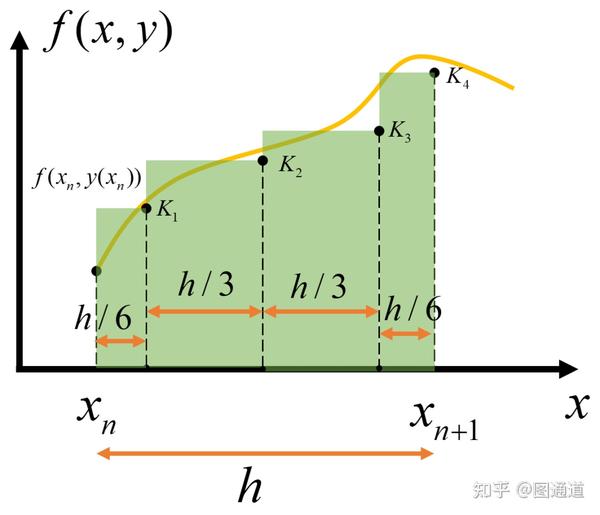
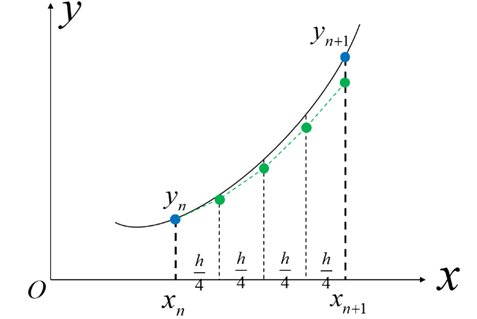
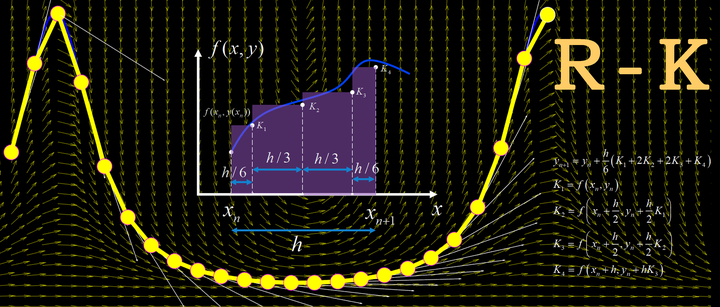
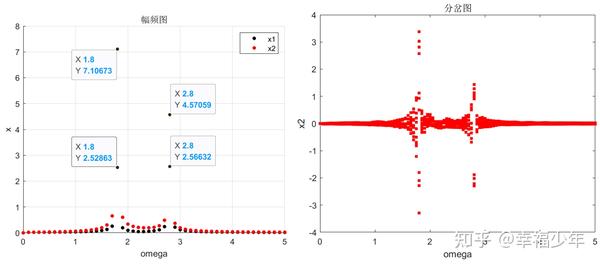
Moonshot回答
龙格-库塔法(Runge-Kutta methods)是一类重要的数值算法,主要用于求解常微分方程(ODEs)的初值问题。它在多个领域有着广泛的应用,包括但不限于:
- 科学与工程领域:用于模拟和解决各种科学和工程问题中的微分方程,如流体动力学、热传递、电磁学等。
- 物理学:用于求解描述物理过程的微分方程,如运动方程、量子力学中的薛定谔方程等。
- 工程领域:在机械、航空、化工等工程领域中,用于设计和分析动态系统。
- 经济学:用于宏观经济模型的仿真,以预测经济趋势。
- 生物学和医学:用于模拟生物过程,如种群动态、药物代谢动力学等。
- 计算机图形学:用于模拟物理现象,如粒子系统、流体模拟等。
龙格-库塔法之所以重要,原因包括:
- 高精度:尤其是四阶龙格-库塔法(RK4),因其较高的精度而被广泛使用。
- 适用性广:适用于从简单到复杂的各种微分方程问题。
- 稳定性:龙格-库塔法具有良好的数值稳定性,可以信赖地用于长期积分。
- 灵活性:可以调整步长以适应不同的问题需求,平衡计算成本和精度。
- 易于实现:算法相对简单,易于在计算机上实现。
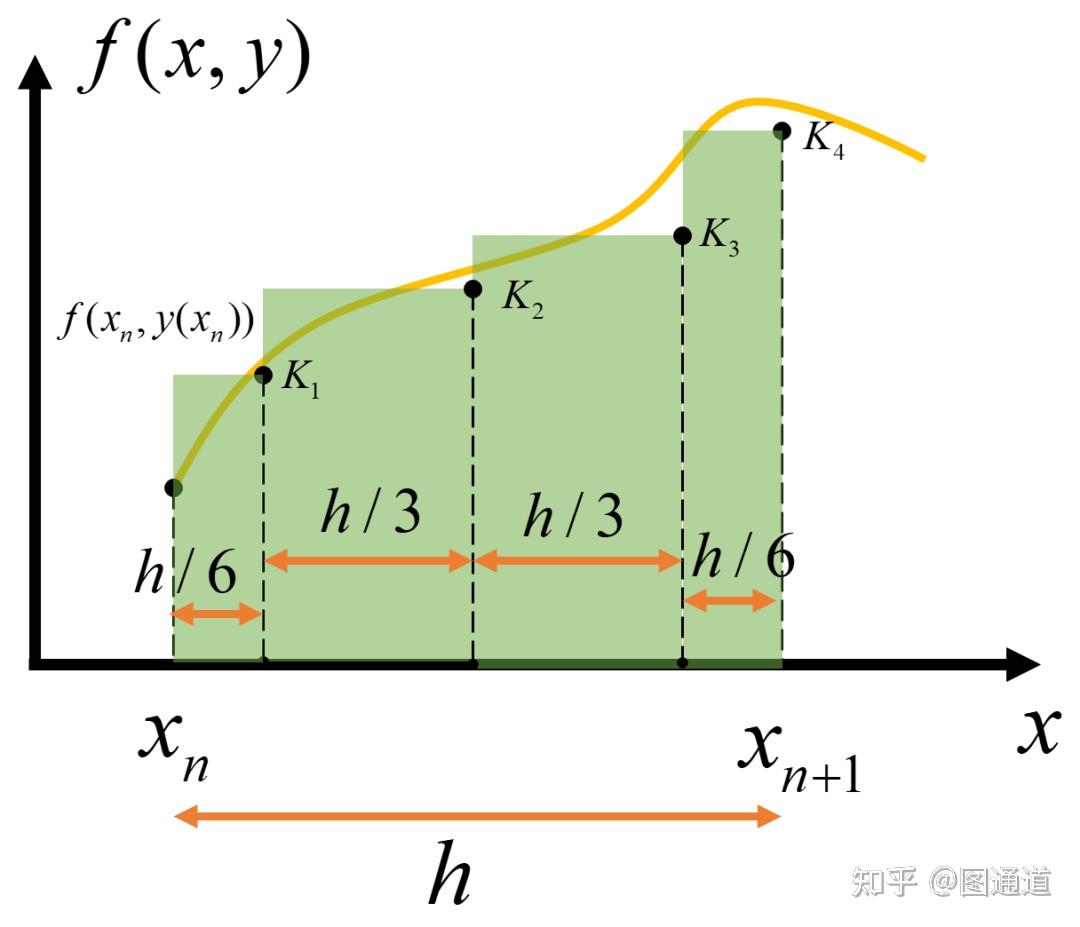
图片来源:龙格-库塔法应用
这些特性使得龙格-库塔法成为解决工程和科学问题中不可或缺的工具。