镜像对称在拓扑弦论中是怎样的概念,它在理论物理学中有什么重要性?
参考资料

-20221102095233874.jpg)
参考资料


-20221102095220140.jpg)
Moonshot回答
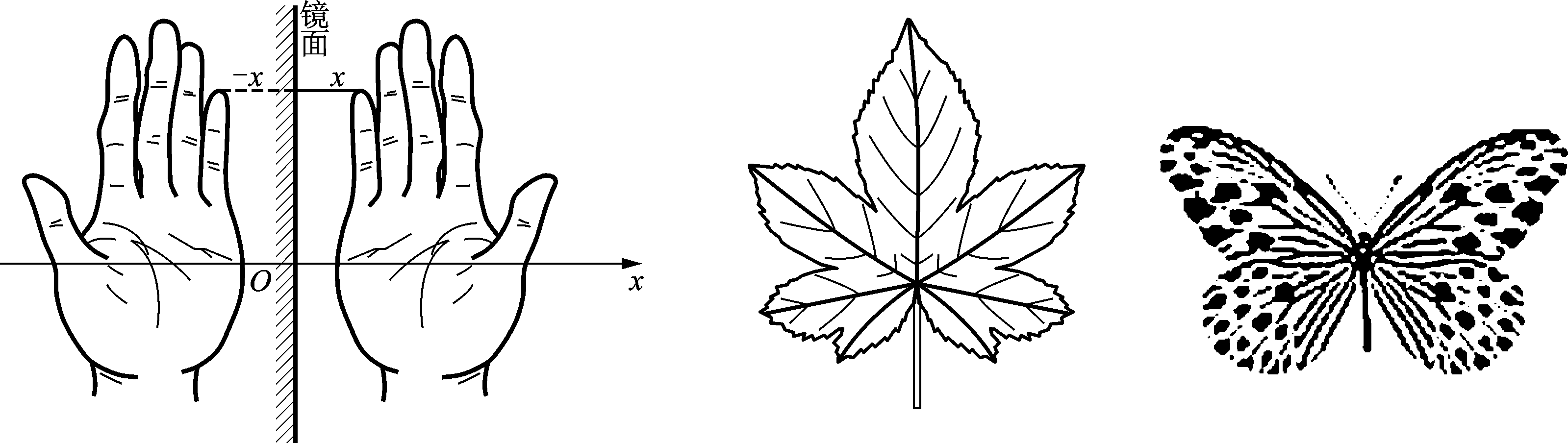
镜像对称在拓扑弦论中是一个核心概念,它描述了两种卡拉比-丘流形(Calabi-Yau manifolds)之间的特殊关系。尽管这两种流形在几何上看起来差异很大,但当它们作为弦理论中的额外维度时,它们在物理上却是等价的。这种关系最早由物理学家发现,并在代数几何和理论物理中具有重要意义。
镜像对称在理论物理学中的重要性体现在多个方面:
- 对偶性:镜像对称提供了一种理解弦理论中不同对偶性的方式,特别是在I型弦和II型弦之间的对偶性。
- 超弦理论:镜像对称在超弦理论中扮演着重要角色,它帮助物理学家理解不同超弦理论之间的关系。
- 数学联系:镜像对称揭示了数学中的代数几何和辛几何之间的深刻联系,促进了数学和物理学的交叉研究。
- 计算物理量:在拓扑弦论中,镜像对称可以用来计算物理量,如格罗莫夫-威滕不变量,这些计算结果编码了完整弦论中的所有全纯量。
- 数学之美:镜像对称展示了数学中的计数几何与物理中的拓扑弦理论之间的联系,体现了数学和物理的内在美。
镜像对称不仅在理论物理学中占有重要地位,也在数学领域产生了深远影响,特别是在代数几何和辛几何的研究中。通过镜像对称,科学家们能够探索和理解更深层次的物理现象和数学结构。