什么是作用量-角度坐标,它在经典力学中有哪些应用?
参考资料

Moonshot回答
作用量-角度坐标是经典力学中一组重要的正则坐标,它在解析可积分系统时具有显著的用途。通过应用作用量-角度坐标,我们无需先解析运动方程式,就能直接求得振动或旋转的频率。这种坐标主要用于完全可分的哈密顿-亚可比方程式,其中哈密顿量显性地不含时间,并且哈密顿量可以表示为作用量变量的函数。
作用量-角度坐标的应用包括但不限于:
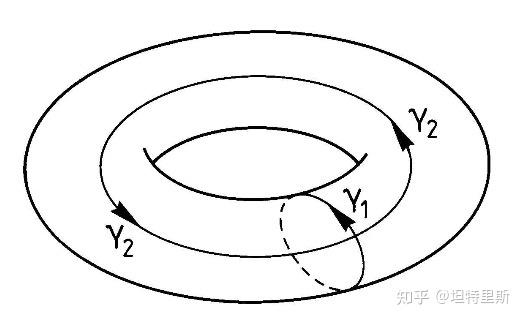
- 定义环面不变量,这在研究系统的长期行为和稳定性时非常重要。
- 促进对完全可分系统的研究,这类系统在数学物理中非常常见。
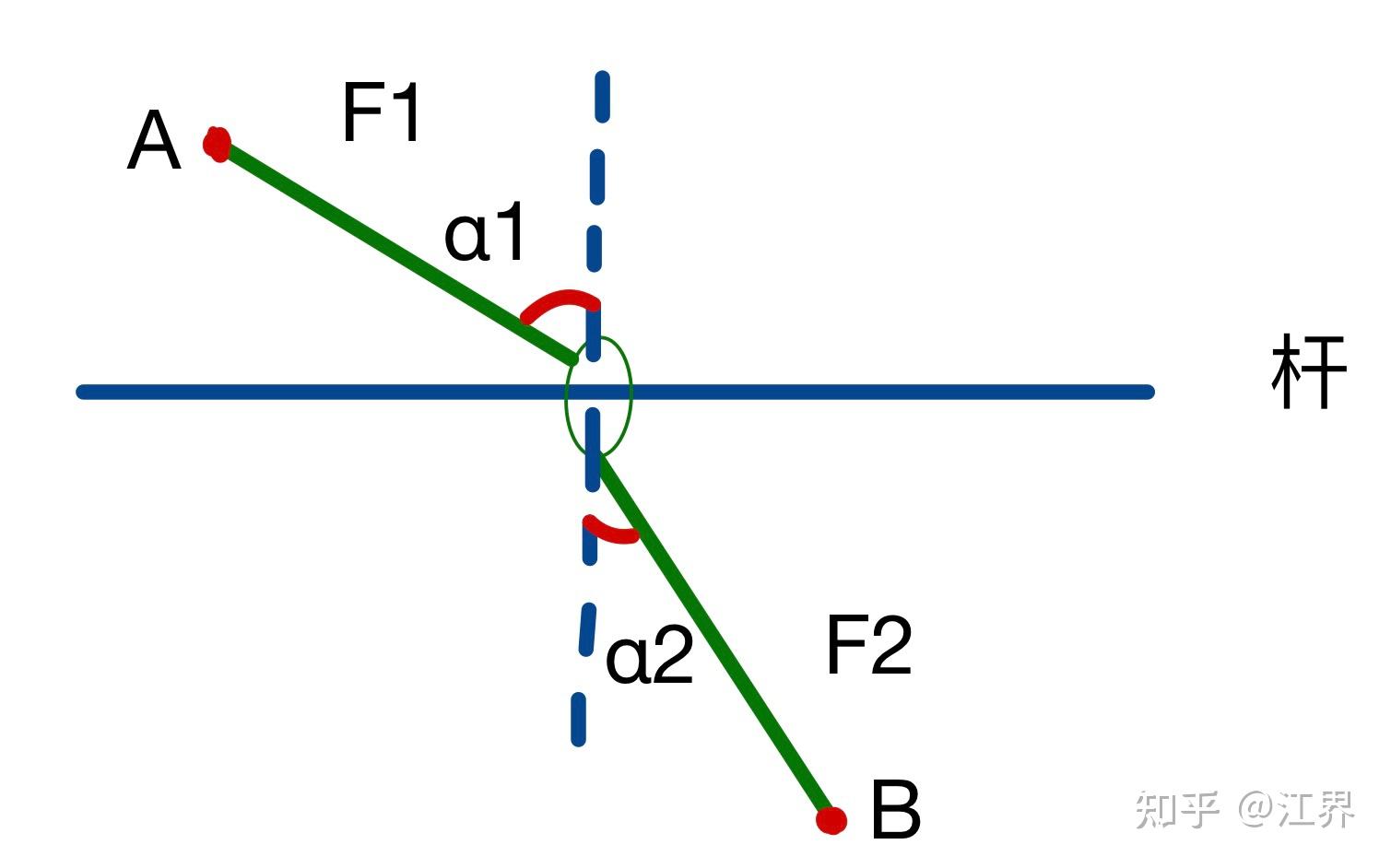
- 帮助计算振动和旋转频率,这在工程和物理问题中非常实用。
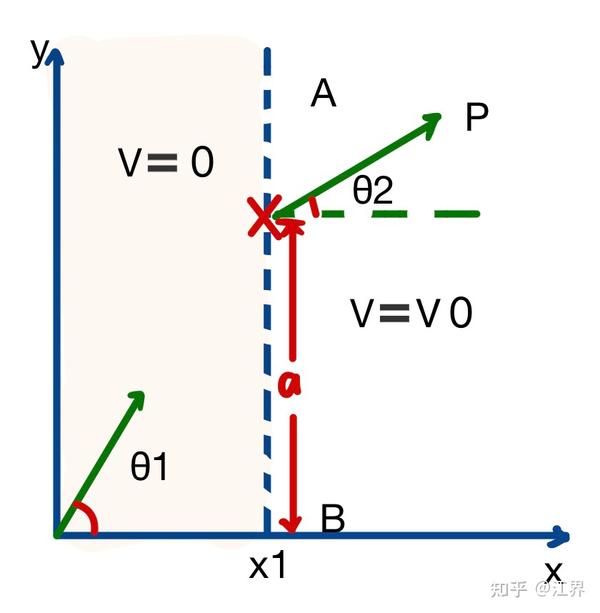
此外,作用量-角度坐标的概念也与最小作用量原理相关,该原理在拉格朗日力学中有重要应用。通过最小作用量原理,我们可以推导出系统的欧拉-拉格朗日方程,进而求解运动方程。

更多详细信息,可以参考维基百科上的作用量-角度坐标条目。
继续提问
相关问题
作用量-角度坐标如何在哈密顿力学中用于处理非线性微扰问题?
波尔-索末菲量子化条件是什么,它与作用量-角度坐标有哪些关系?
黑神话悟空是用什么编程语言编写的
砂拉越反让渡运动中,英国政府采取了哪些措施来削弱反让渡运动的影响力?
林爽文事件是台湾历史上的一次重要农民起义,它的结局如何?
圣克里斯托瓦尔山的圣母雕像在历史上是否经历过其他重大修复或者变化,除了2012年那次清洁和重新涂色?
在英格兰的55座城市中,哪些城市的城市地位是在20世纪或之后授予的?
葡萄牙伯国的两个不同时期分别是什么?它们之间有何区别?
经典动画《白雪公主》中,七个小矮人的角色设计和动画制作有哪些幕后故事?
第56届奥斯卡金像奖的颁奖典礼在什么地点举行,该地点还承办过几届奥斯卡颁奖典礼?