格拉斯曼数在费米子场路径积分中的作用是什么,为什么必须用到格拉斯曼数来描述费米子?
参考资料


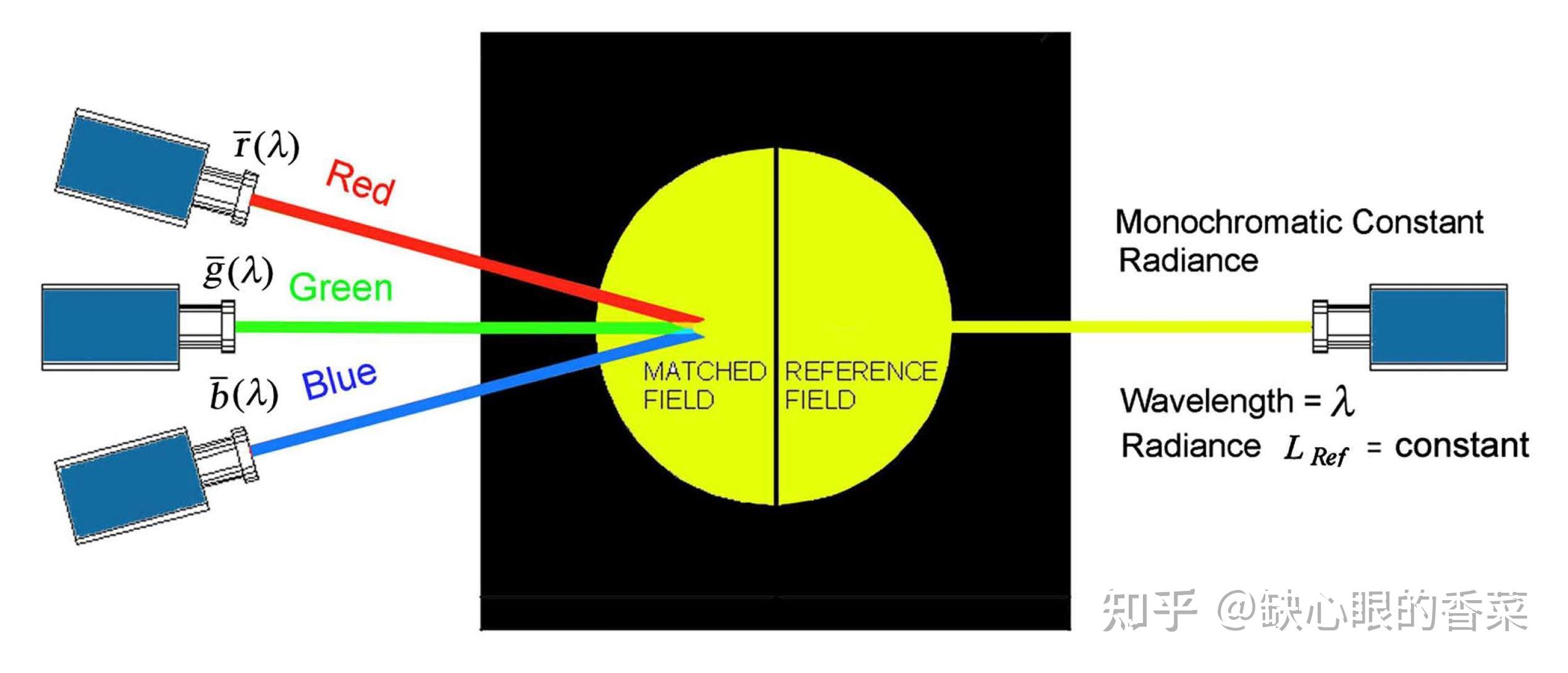
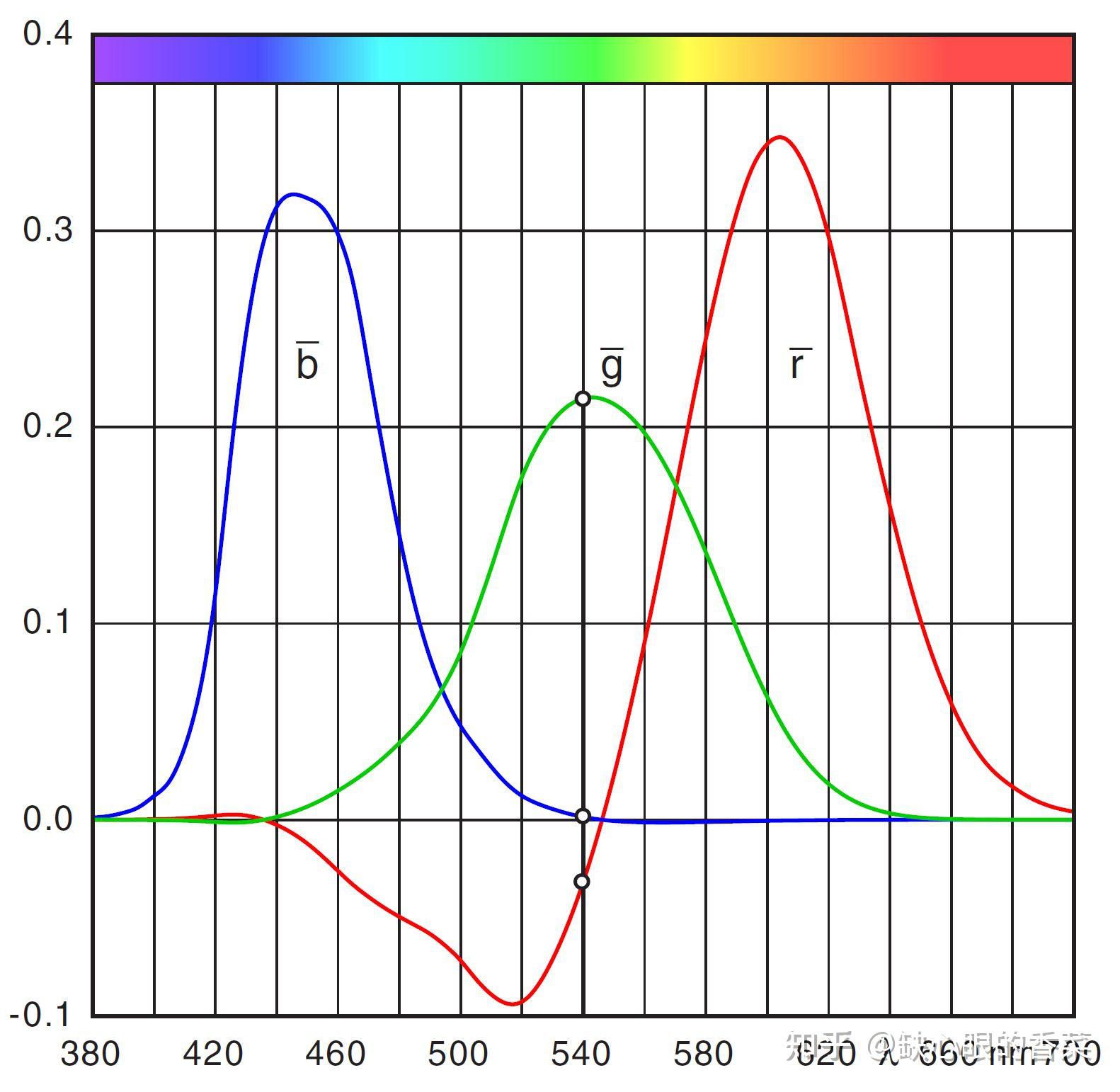
参考资料
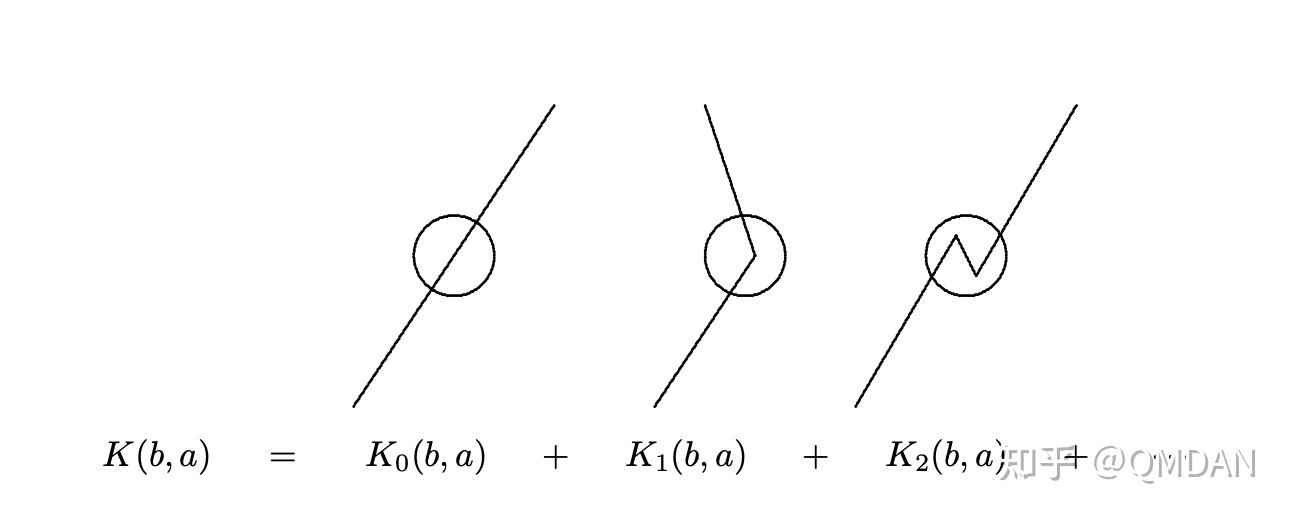
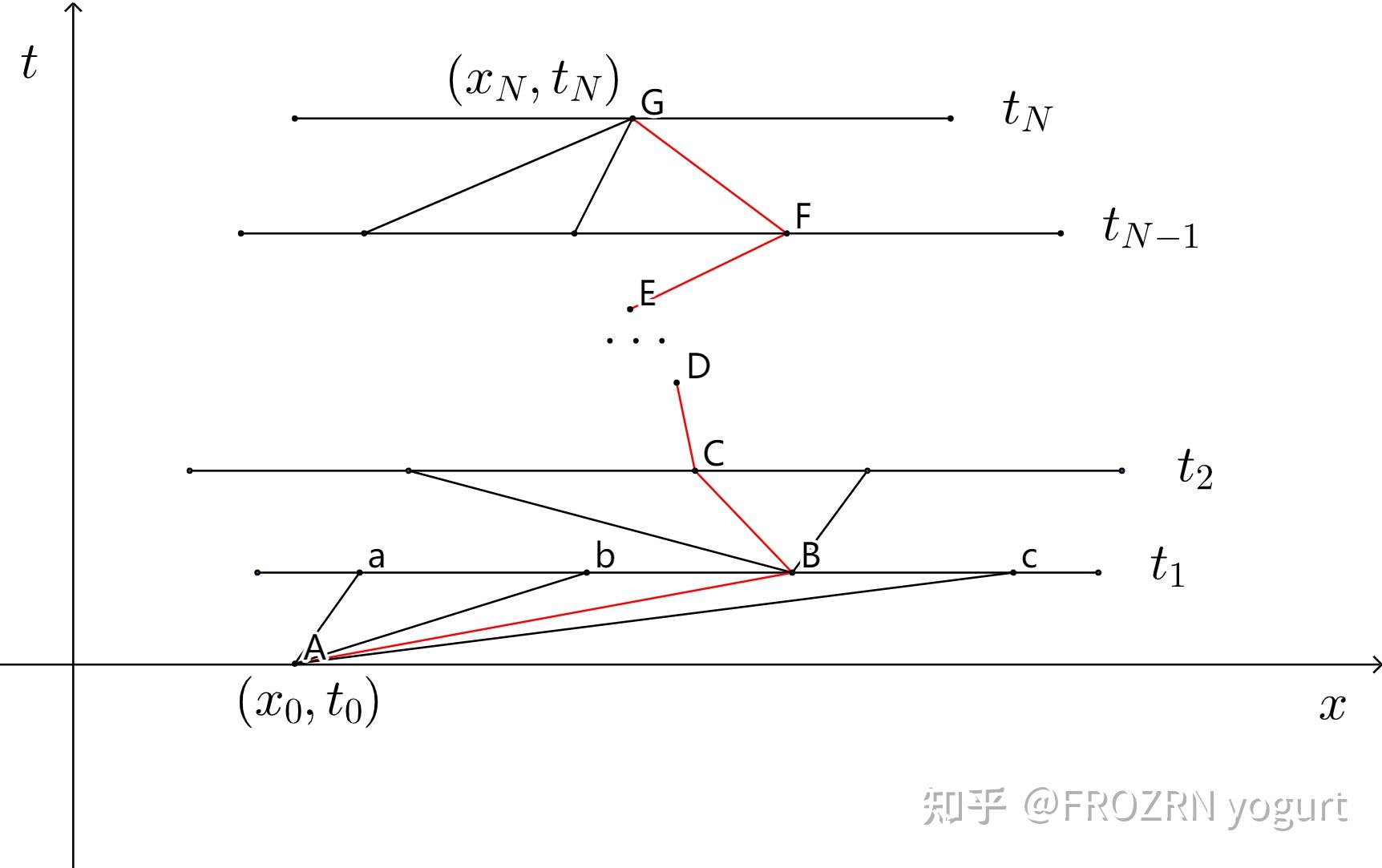


Moonshot回答
格拉斯曼数在费米子场路径积分中的作用是至关重要的。它们是量子场论中反交换算符的“经典类比”,用于定义费米子场的路径积分。由于费米子具有反对易性,即同一状态不能有两个或更多相同的费米子,因此需要格拉斯曼数来正确描述费米子的路径积分。格拉斯曼数的积分,也称为别列津积分,具有线性和分部积分公式的特性,这使得费米子场的路径积分能够被正确计算。
此外,格拉斯曼数在超流形或超空间的定义中也有重要用途,它们被用作“反交换坐标”。这种数学结构对于描述费米子的物理性质是必要的,因为它们能够捕捉到费米子的反对易性,这是玻色子所不具备的。因此,格拉斯曼数不仅在数学上是有用的工具,而且在物理上也是描述费米子行为的关键要素。
继续提问
相关问题
洛杉矶火花如何在WNBA联赛中保持竞争力,他们的管理层和教练在这方面做了哪些努力?
德克萨斯心跳法案对周边州的堕胎人数产生了怎样的影响,为什么会导致这些变化?
漫画《星守犬》共多少卷、多少话,具体连载时间是什么时候?
《超人:钢铁英雄》的编剧是谁,他还参与过哪些有名的电影作品?
为什么克里斯蒂娜·英格斯多塔被视为内尔迪察教堂中的圣克里斯蒂娜?
《感染》电影是由哪家公司发行的,该公司还有哪些著名发行电影?
图尔库作为芬兰最古老的城市,它的历史可以追溯到哪个世纪?
什么是涵数,如何在量子力学中定义和应用它们?
尼古拉·沃兹涅先斯基在苏联战后经济恢复中扮演了什么关键角色?
《恋爱无尽》在第66届威尼斯电影节上获得了哪些提名和奖项?