参考资料

在三维空间中，两个向量的叉积结果与参与运算的两个向量有以下关系：

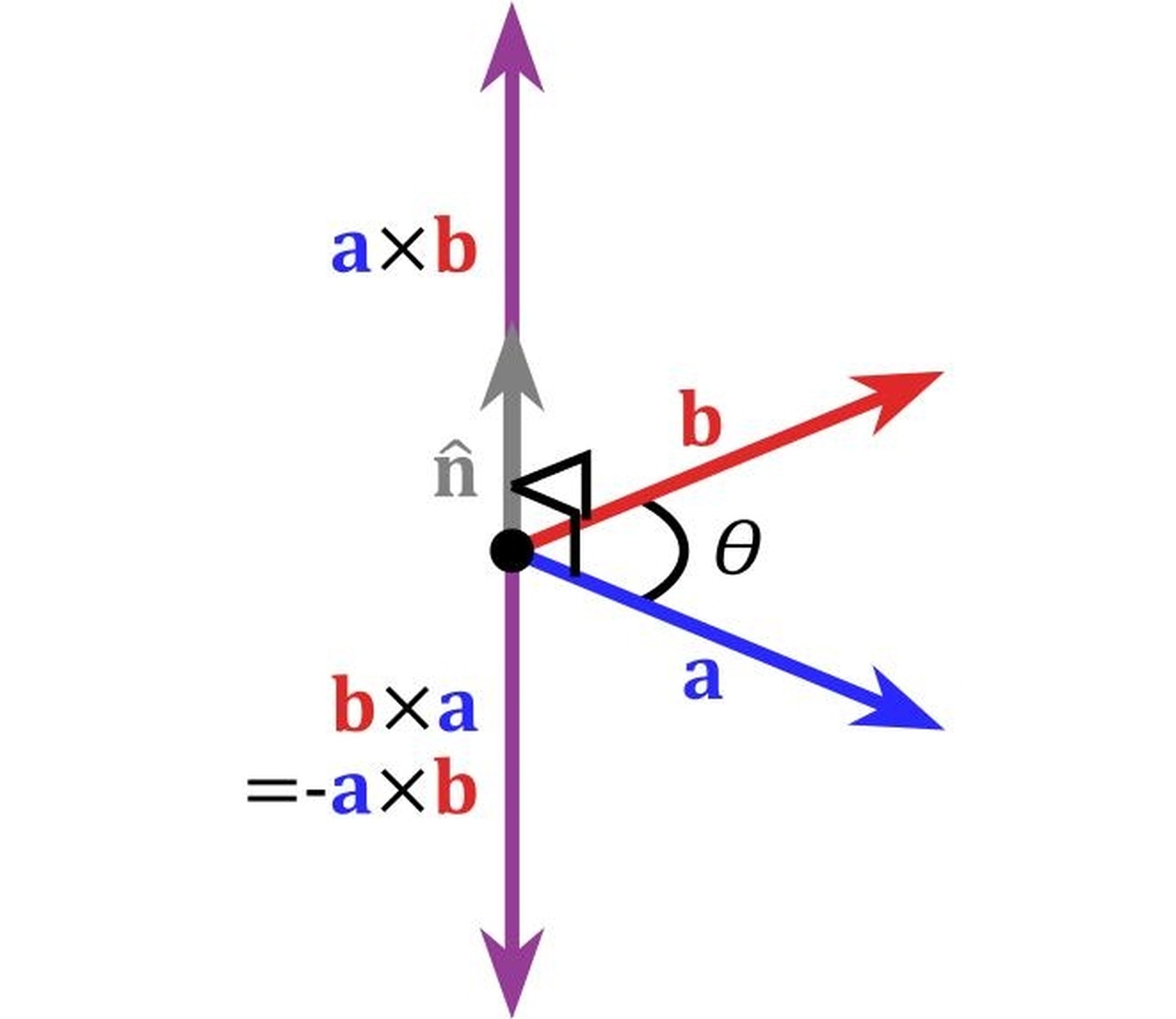
1. 方向：叉积结果向量垂直于参与运算的两个向量所定义的平面，遵循右手法则。这意味着如果你用右手的四指从第一个向量以最短角度转向第二个向量，你的拇指将指向叉积向量的方向。

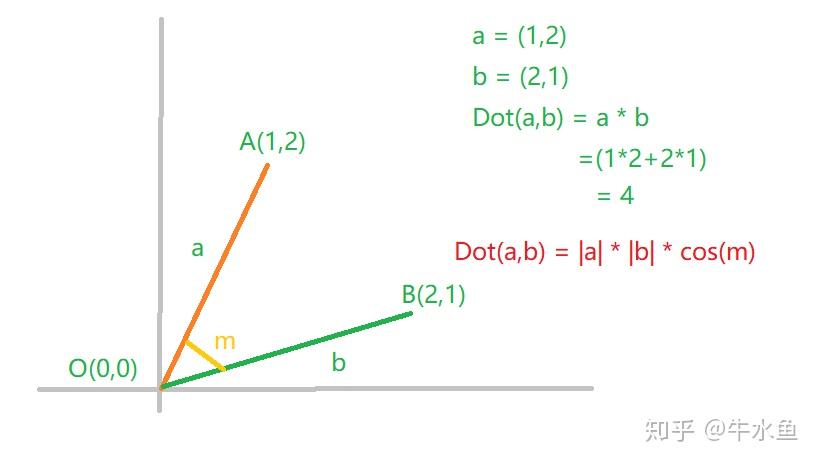
2. 大小：叉积结果向量的大小等于两个向量模的乘积与它们之间夹角的正弦值。数学上表示为 ( |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}||\mathbf{b}|\sin(\theta) )，其中 ( |\mathbf{a}| ) 和 ( |\mathbf{b}| ) 分别是向量 ( \mathbf{a} ) 和 ( \mathbf{b} ) 的模，( \theta ) 是它们之间的夹角。

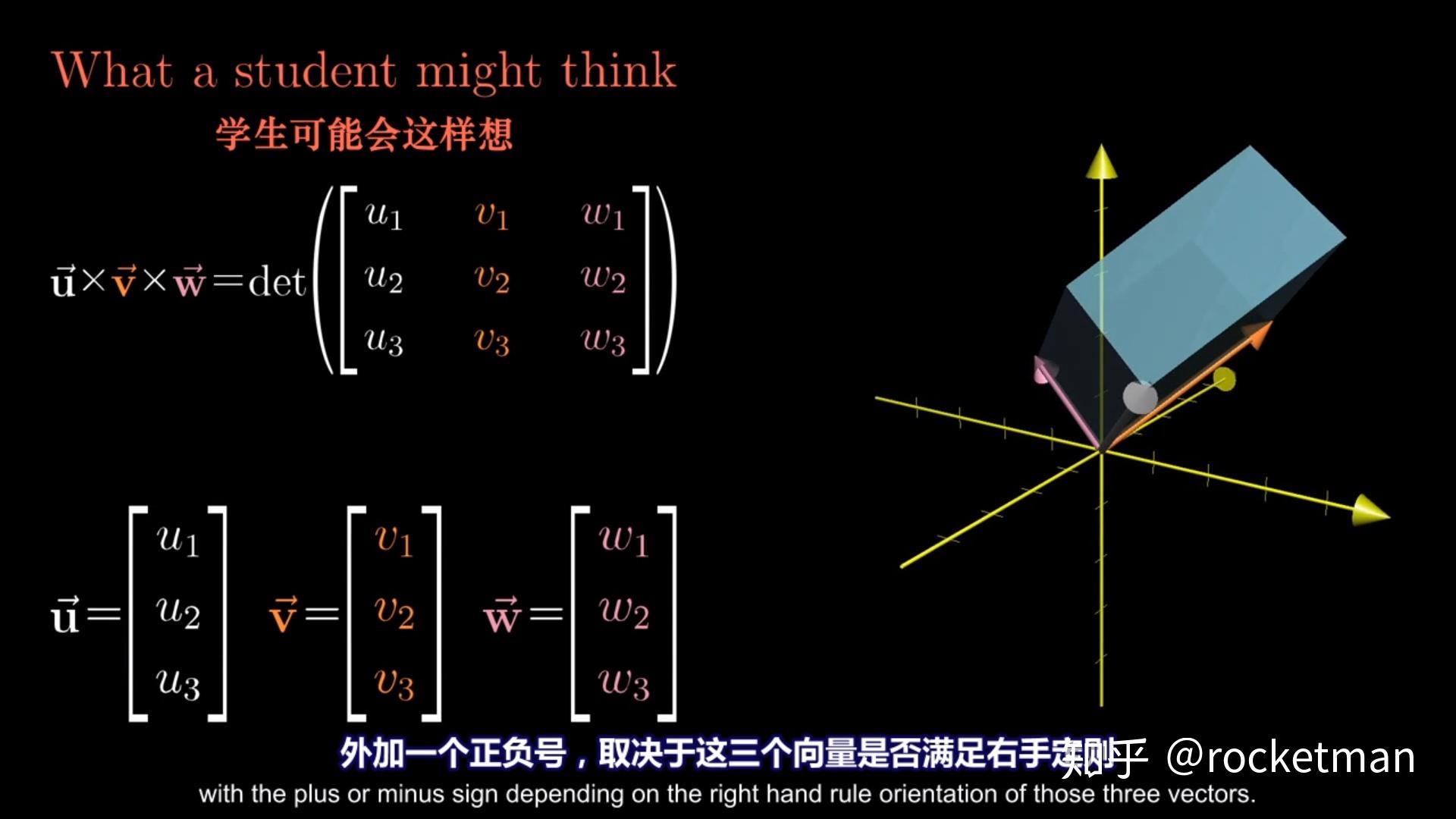
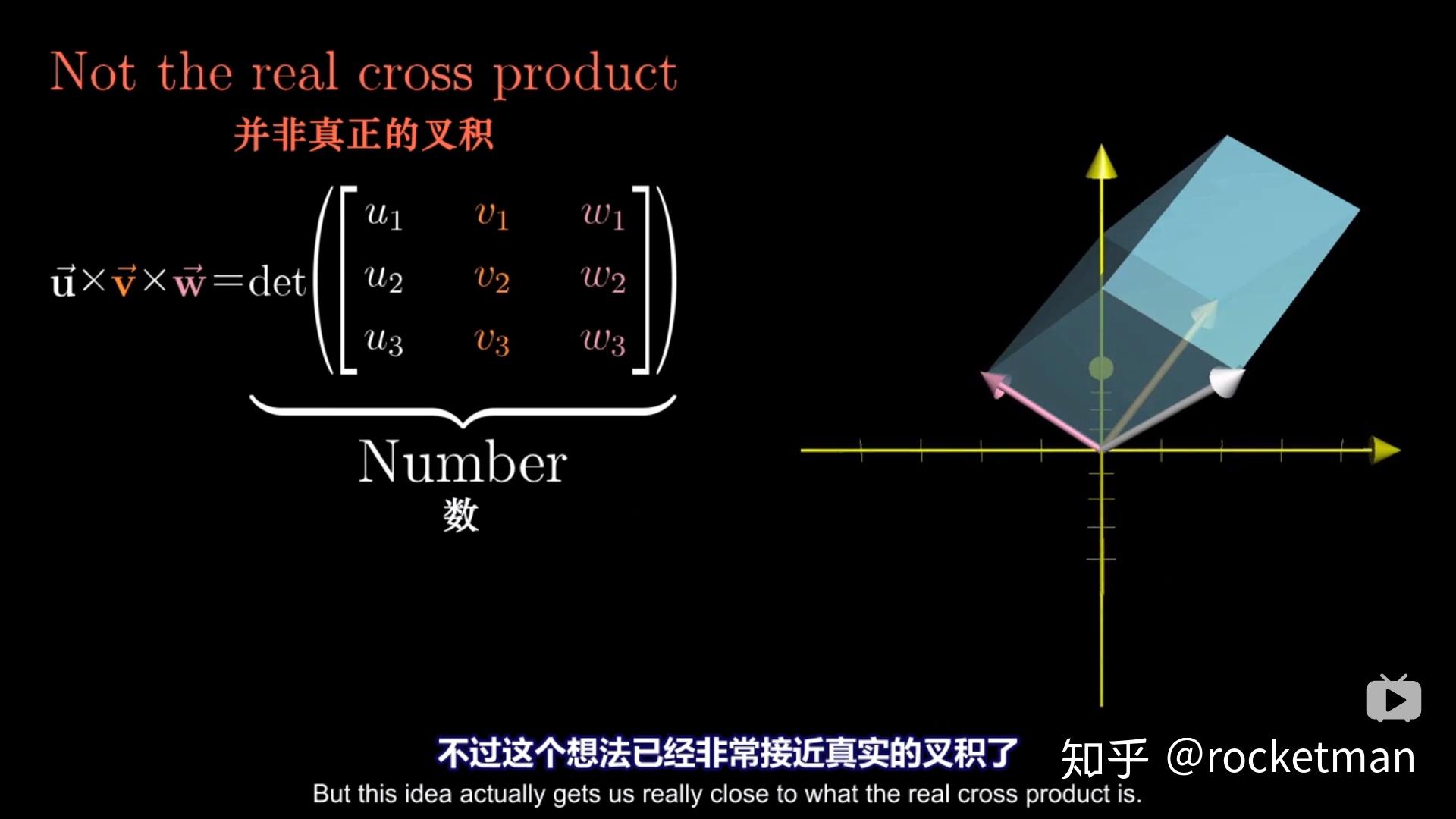
3. 几何意义：叉积的模长代表由两个向量构成的平行四边形的面积。如果两个向量是共线的，那么它们的叉积为零向量，因为共线向量构成的平行四边形面积为零。

4. 反交换律：叉积满足反交换律，即 ( \mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a}) )。

5. 与点积的关系：叉积与点积可以通过向量三重积恒等式联系起来，例如 ( \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = \mathbf{b} \cdot (\mathbf{c} \times \mathbf{a}) = \mathbf{c} \cdot (\mathbf{a} \times \mathbf{b}) )。

这些性质在物理学和工程学中非常重要，例如在计算力矩和角动量时。通过搜索结果，我们可以看到这些性质在不同的上下文中被讨论，如在极客教程中对叉积的定义和性质的描述，以及在CSDN博客中对叉积几何意义的解释。这些资源提供了丰富的信息来帮助理解叉积与参与运算的向量之间的关系。