波尔-索末菲量子化条件是什么,它与作用量-角度坐标有哪些关系?
参考资料



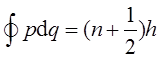
参考资料
Moonshot回答
波尔-索末菲量子化条件是旧量子论中的一个重要概念,由尼尔斯·玻尔和阿诺·索末菲提出。它基于玻尔模型,对原子中电子的轨道进行了量子化处理。根据搜索结果,波尔-索末菲量子化条件可以表述为:当量子数n趋于无穷大时,量子化的能级将趋于经典的连续能量,量子化理论将趋于经典理论。索末菲数(常用希腊字母α表示)表示电子在第一玻尔轨道上的运动速度和真空中光速的比值,计算公式为 α=e²/(4πε₀cħ),其中e是电子的电荷,ε₀是真空介电常数,ħ是约化普朗克常数。
作用量-角度坐标是经典力学中一组正则坐标,通常在解析可积分系统时具有很大用处。应用作用量-角度坐标的方法,不需要先解析运动方程式,就能够求得振动或旋转的频率。作用量-角度坐标主要用于完全可分的哈密顿-亚可比方程式(哈密顿量显性地不含时间,也就是说,能量保持恒定)。
波尔-索末菲量子化条件与作用量-角度坐标的关系在于,它们都试图在经典物理和量子物理之间架起桥梁。波尔-索末菲条件通过量子化电子轨道来解释原子光谱,而作用量-角度坐标提供了一种在经典力学框架内处理振动和旋转问题的方法。两者都体现了物理学家试图用量子理论来解释和预测经典物理现象的努力。尽管旧量子论最终被量子力学所取代,但波尔-索末菲量子化条件和作用量-角度坐标在物理学史上仍具有重要地位,为后来的量子力学发展奠定了基础。