参考资料

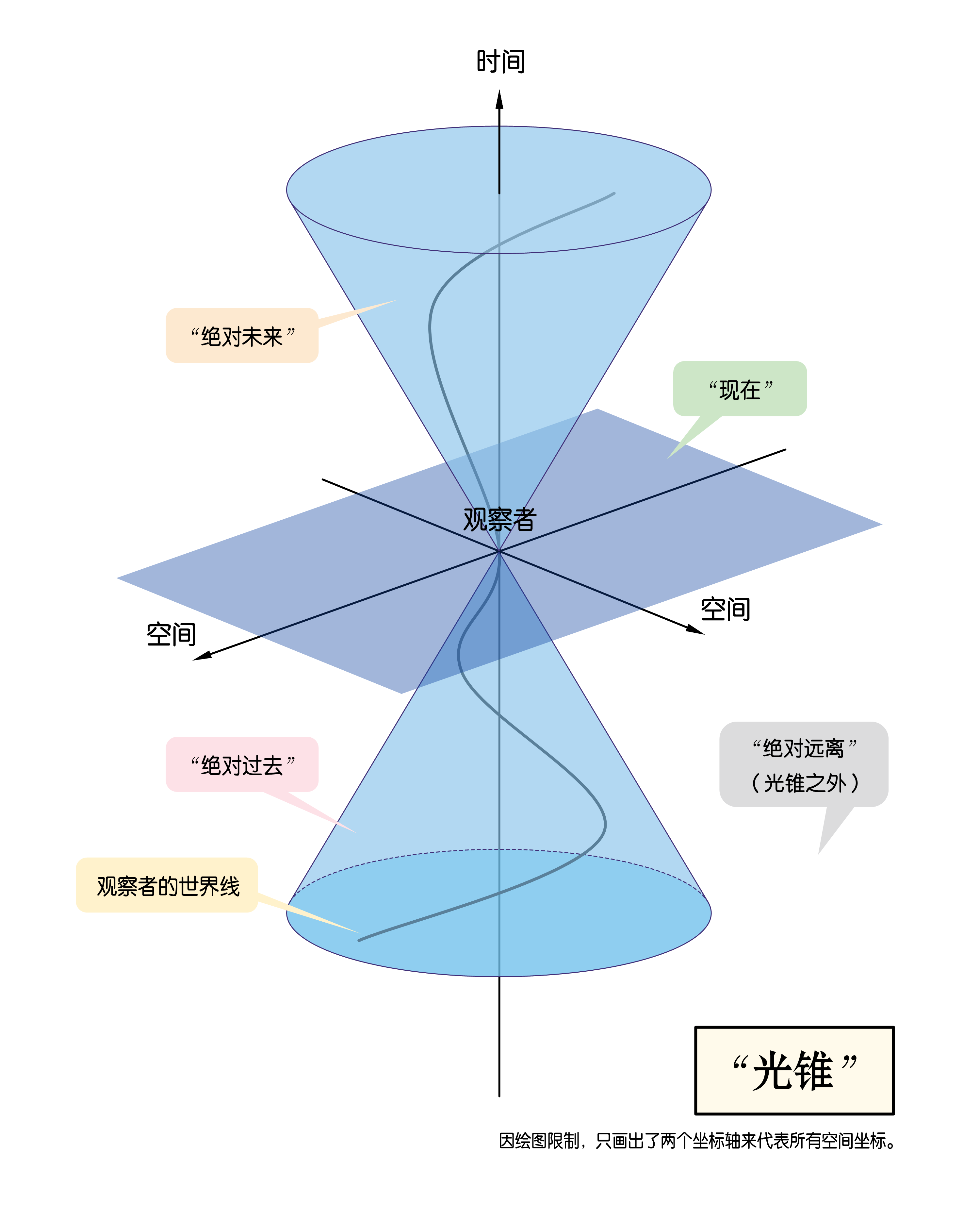
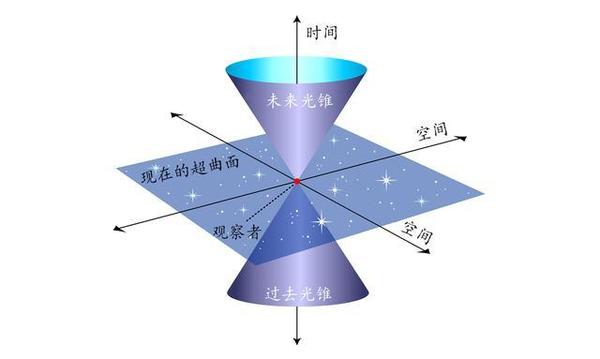
四维时空旋转对称性是物理学中一个重要的概念，它包括了时空平移变换和洛伦兹变换两大类。在物理学中，四维时空旋转对称性的应用非常广泛，例如：

1. 洛伦兹变换：从四维时空的角度解释洛伦兹变换和相对论的许多特征。洛伦兹变换描述了在不同惯性参考系之间的空间和时间坐标如何转换，这与三维空间中的旋转不同，因为两个时空轴以剪刀般的方式对称地相互旋转。

2. Poincare群（变换）：这是四维时空的对称变换群，包括了时空平移和旋转。在场论或凝聚态物理中，Poincare群的变换通常被用来描述物理系统的对称性。

3. 守恒定律：对称性与守恒定律紧密相关。例如，能量守恒、动量守恒和角动量守恒都可以从时空对称性中导出。

4. 量子力学：在量子力学中，时间平移对称性的自发破缺可能导致新奇的物理现象，如量子时间晶体。

5. 氢原子模型：具有SO(4)对称性的氢原子模型可以精确求解，展示了特殊对称性在解决物理问题中的重要性。

6. 闵可夫斯基时空：这是由三维欧几里得空间与时间组成的四维流形，其中任意两个事件之间的时空间隔与所依照的惯性参考系无关，是狭义相对论的基础。

四维时空旋转对称性不仅在理论物理学中扮演着核心角色，也在现代物理学的许多领域，如量子场论、粒子物理学和宇宙学中有着深远的影响。通过引用的搜索结果，我们可以更深入地理解这一概念及其在物理学中的应用。