分形理论是什么，分形理论在数学研究中有哪些应用？
参考资料
参考资料
Moonshot回答
分形理论是由美籍数学家本华·曼德博（Benoit B. Mandelbrot）在20世纪70年代末提出的，它是一种研究复杂几何形状的数学理论。分形理论的核心在于用分数维度的视角和数学方法描述自然界中的复杂形状，这些形状通常表现出自相似性，即在不同的尺度上重复出现相似的模式。
在数学研究中，分形理论有广泛的应用，包括但不限于以下几个方面：
- 分形维数的计算：分形维数是描述分形对空间填充程度的统计量，有多种计算方法，如Hausdorff维数、盒维数等。
- 分形图形的生成：通过迭代算法生成各种分形图形，如Mandelbrot集和Julia集。
- 分形生长模型与模拟：模拟自然界中的生长过程，如植物的分枝、河流的流域形成等。
- 分形插值与模拟：在数值分析中，利用分形理论进行数据插值和模拟。
- 随机分形：研究随机过程中的分形结构，如自然界中的粗糙表面或云彩的形状。
- 与混沌理论的交叉：分形理论与混沌理论相结合，研究动态系统中的复杂行为。
此外，分形理论在其他领域也有应用，如计算机科学、艺术设计、经济学等。例如，在计算机图形学中，分形理论被用来生成逼真的自然景观；在艺术设计中，分形图案因其独特的美学价值而被广泛采用。
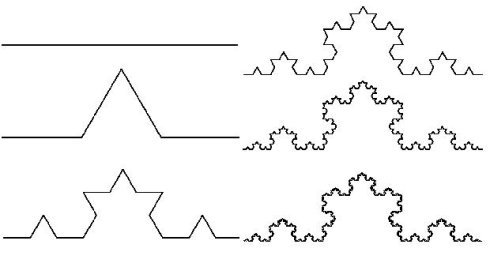
一个展示分形理论在数学研究中应用的示例图
分形理论不仅展示了数学之美，也揭示了世界的本质，改变了人们理解自然奥秘的方式。通过分形理论，数学家们能够以一种全新的视角来探索和描述自然界中的复杂现象。