参考资料
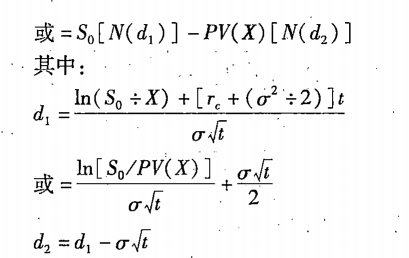


Moonshot回答
布莱克-斯科尔斯模型(Black-Scholes Model)是一个用于定价欧式期权的数学模型,由费舍尔·布莱克(Fischer Black)、米伦·斯科尔斯(Myron Scholes)以及罗伯特·默顿(Robert Merton)在20世纪70年代提出。该模型通过计算衍生品组合来实现完美对冲,主要基于以下假设:
- 股价遵循对数正态分布,且变化是连续的。
- 无风险利率和波动率是恒定的。
- 没有交易成本和税收。
- 允许无限制地卖空股票。
- 期权只能在到期时行使(欧式期权)。
在实际操作中,投资者会构建一个由标的资产(如股票)和期权合约组成的组合。通过调整组合中期权和标的资产的数量,使得组合的价值对标的资产价格的小幅变动不敏感,即实现Delta中性。Delta是期权价格相对于标的资产价格变动的敏感度。当组合达到Delta中性时,无论股价如何小幅波动,组合的价值都能保持不变,从而实现完美对冲。
此外,为了维持这种对冲状态,投资者需要不断地调整组合中期权和标的资产的数量,这个过程称为动态对冲。虽然在实际操作中,由于市场条件的变化,完美对冲很难长期维持,但布莱克-斯科尔斯模型提供了一个理论上的框架来指导对冲操作。
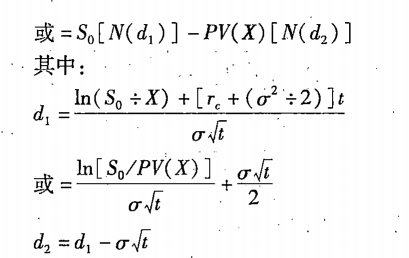
引用来源:
继续提问
相关问题
布莱克–斯科尔斯–默顿期权定价模型如何改变了金融衍生品市场的计算方法,并促进了期权市场的快速发展?
布莱克-舒尔斯模型中的风险中性假设在实际应用中如何被质疑和调整?
金融经济学家为何容易忽视布莱克-舒尔斯公式的实用交易策略版本与理论版本的区别?
为什幺尽管知道布莱克-舒尔斯模型有局限性,金融从业者仍依赖这个模型进行定价?
是什么是等熵(可逆绝热)过程,在卡诺循环中它的作用是什么?
哪些具体的技术解决方案被认为对提升教育质量有显著帮助,并逐渐被广泛接受?
慈禧太后是如何在晚清时期独掌大权,成为实际统治者的?
斯莱特行列式在自洽场方法和HF方程中的应用是怎样的?
军工行业在全球经济波动中的表现为何相对稳定?
法越关系在明命时期为何恶化,导致法国对越南的侵略?