参考资料

Moonshot回答
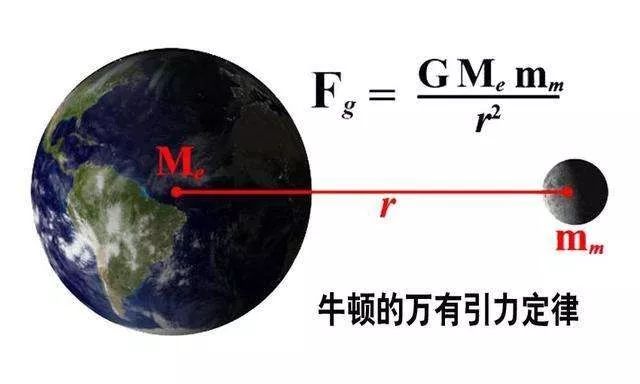
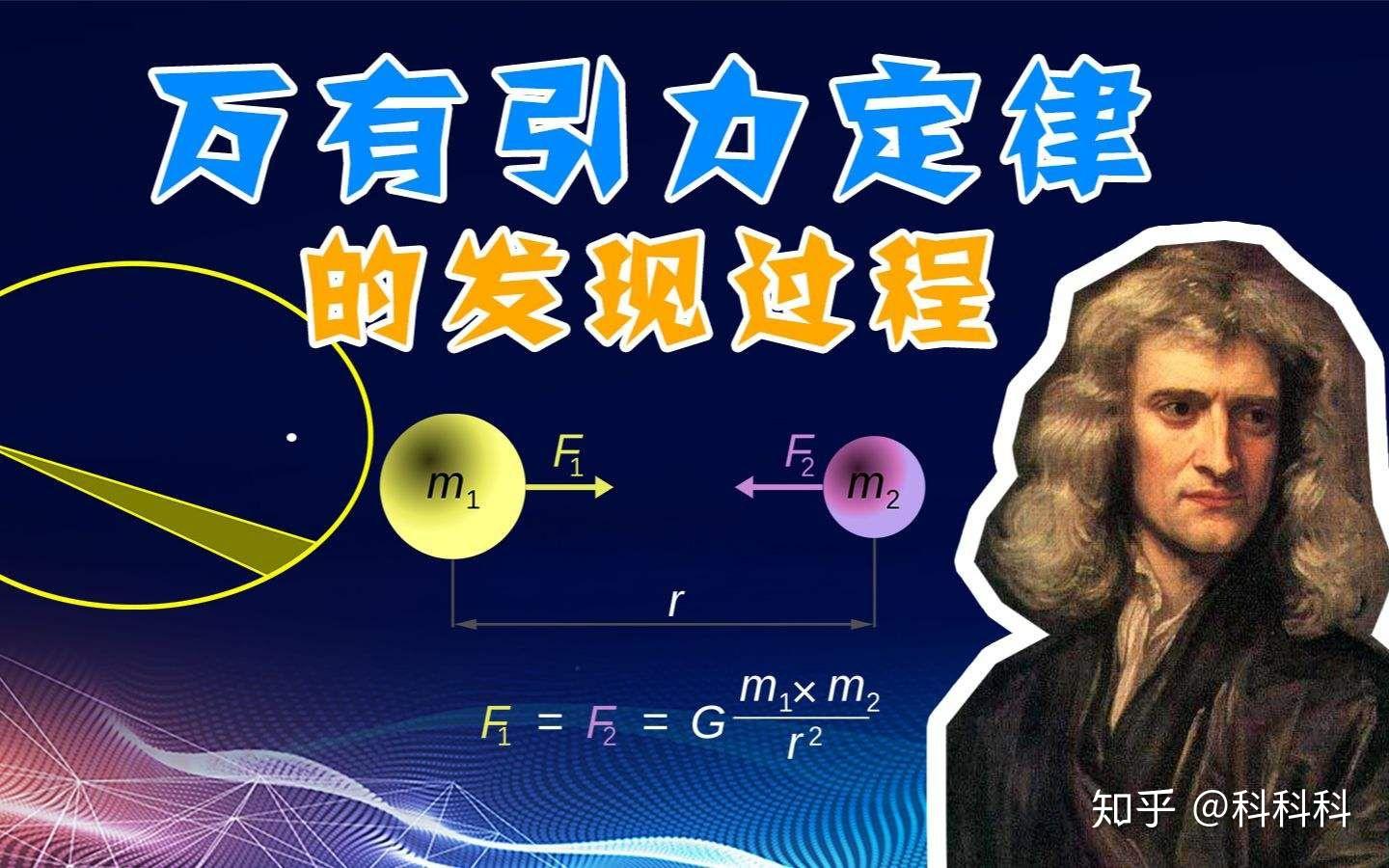
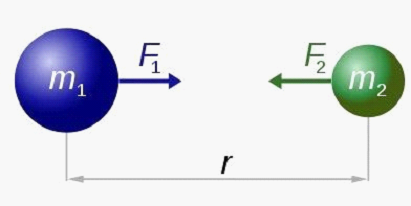
牛顿的万有引力定律表明,两个物体之间的引力与它们的质量乘积成正比,与它们之间距离的平方成反比。这里的“距离平方定律”具体指的是,当两个物体之间的距离增加时,它们之间的引力会随着距离的平方增加而减少。例如,如果两个物体之间的距离加倍,它们之间的引力将减少到原来的四分之一(因为 (2^2 = 4))。这个定律可以用数学公式表示为:
[ F = G \frac{m_1 m_2}{r^2} ]
其中 ( F ) 是两个物体之间的引力,( G ) 是万有引力常数,( m_1 ) 和 ( m_2 ) 是两个物体的质量,( r ) 是它们之间的距离。这个定律不仅适用于地球和月球这样的天体,也适用于任何两个有质量的物体。

这个定律是艾萨克·牛顿在1687年发表的《自然哲学的数学原理》中提出的,它解释了行星运动的规律,并且对物理学和天文学产生了深远的影响。根据搜索结果,这个定律表述如下:任何两个质点都存在通过其连心线方向上的相互吸引的力。该引力大小与它们质量的乘积成正比,与它们距离的平方成反比,与两物体的化学组成和物理状态无关。来源
继续提问
相关问题
1997年地震对亚西西的圣方济各圣殿造成了哪些破坏?
朱祁鐄的王妃李氏患有痼疾后,朝廷为什么同意为他再次择配官宦及良家之女?
《那年男孩》电影获得了多少越南盾的票房收入?
为什么中华民国大陆时期的农村经济在大萧条时期受到了严重打击?
多用户系统中,用户家目录的设计是如何确保其他用户无法接触其文件的?
公司对薪资相关的税款和福利的支付分配是怎样的,员工负担什么样的税费和福利?
人头录音技术如何实现360度的声场效果?
量子力学中的对易关系与经典物理学中的变量关系有什么不同?
伊琳娜·安格丽娜与菲利普·冯·施瓦本的婚姻是如何被历史学家记录的?这些记录揭示了哪些历史细节?
《第三种爱情》的主题曲叫什么名字,谁演唱的?